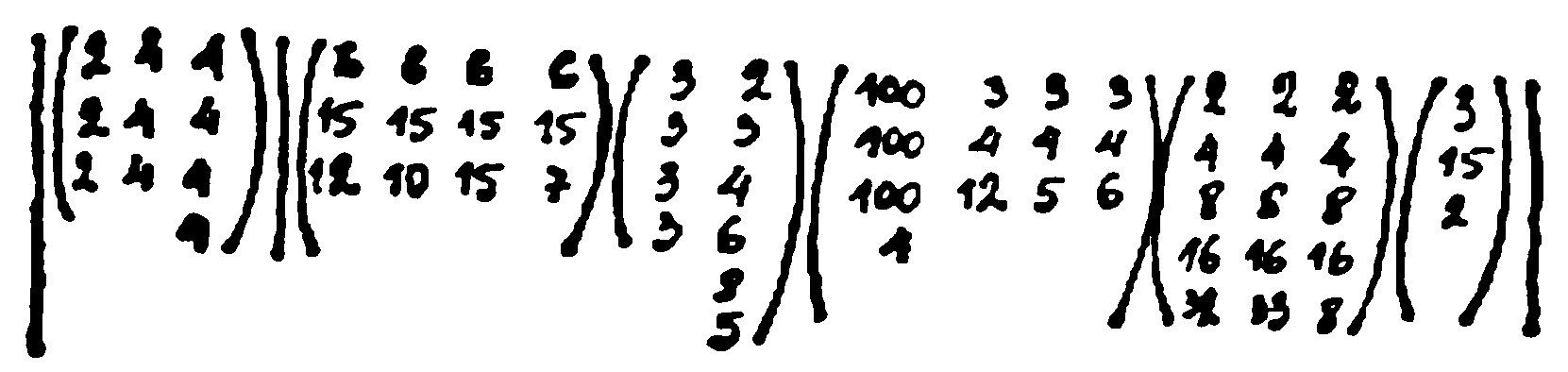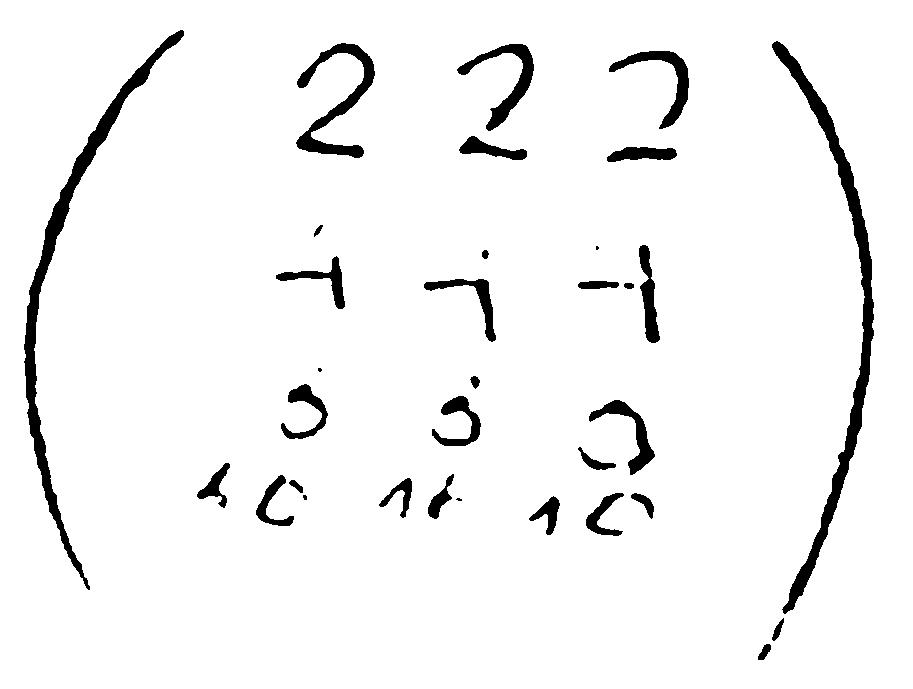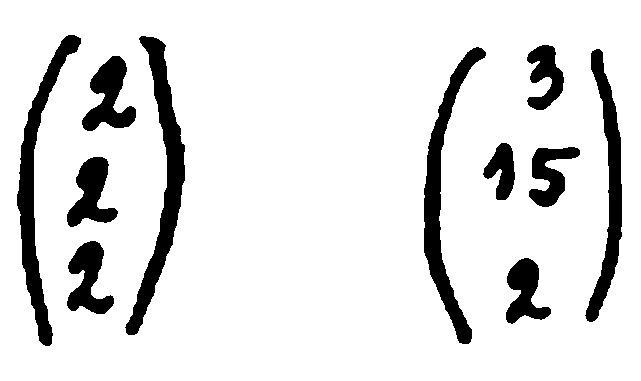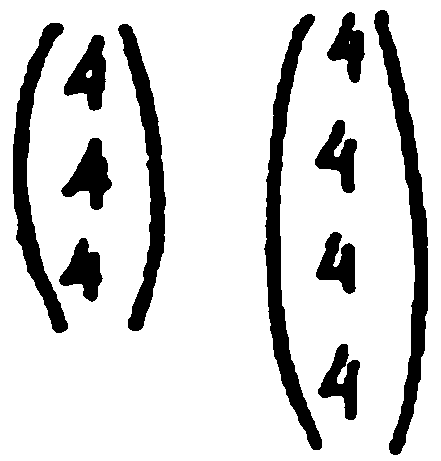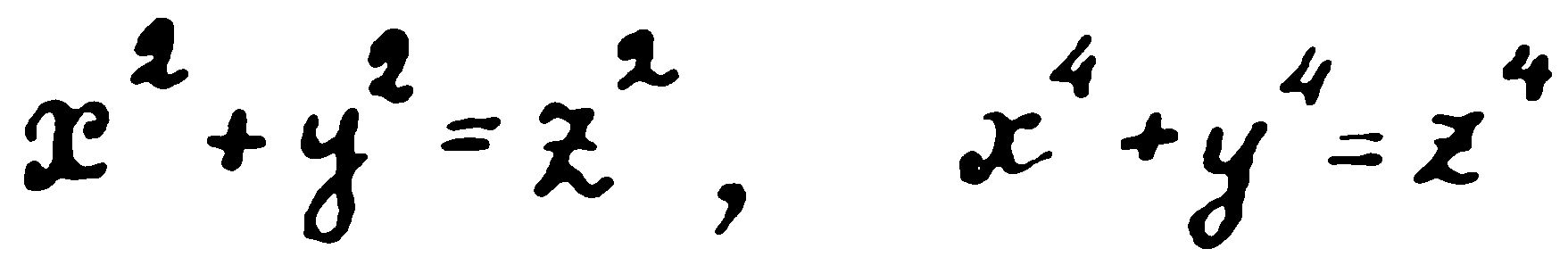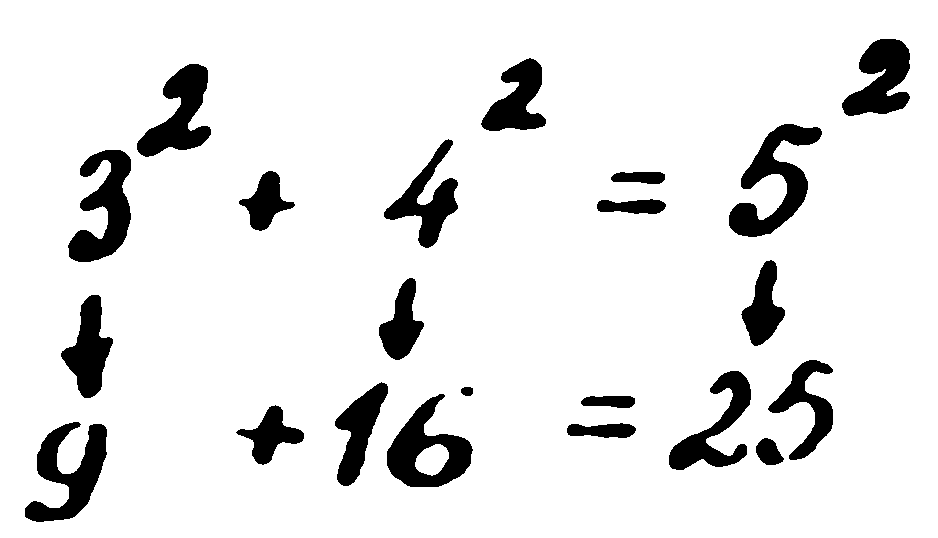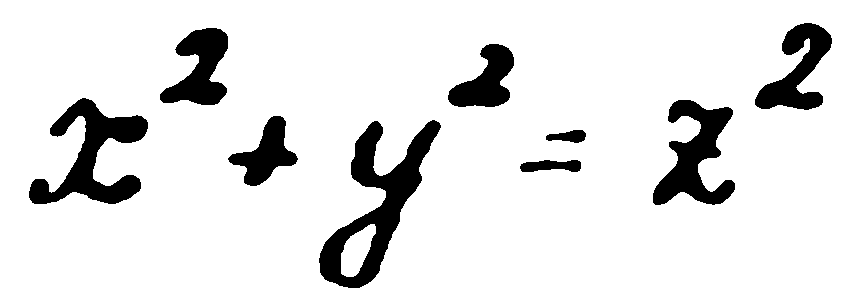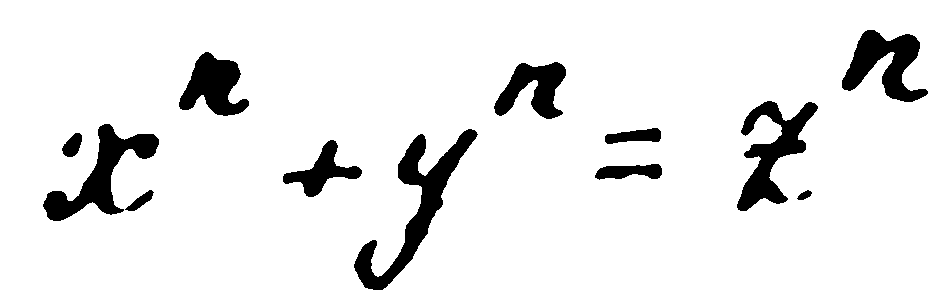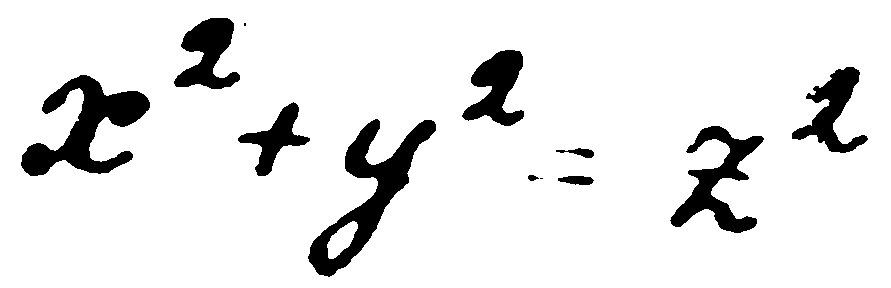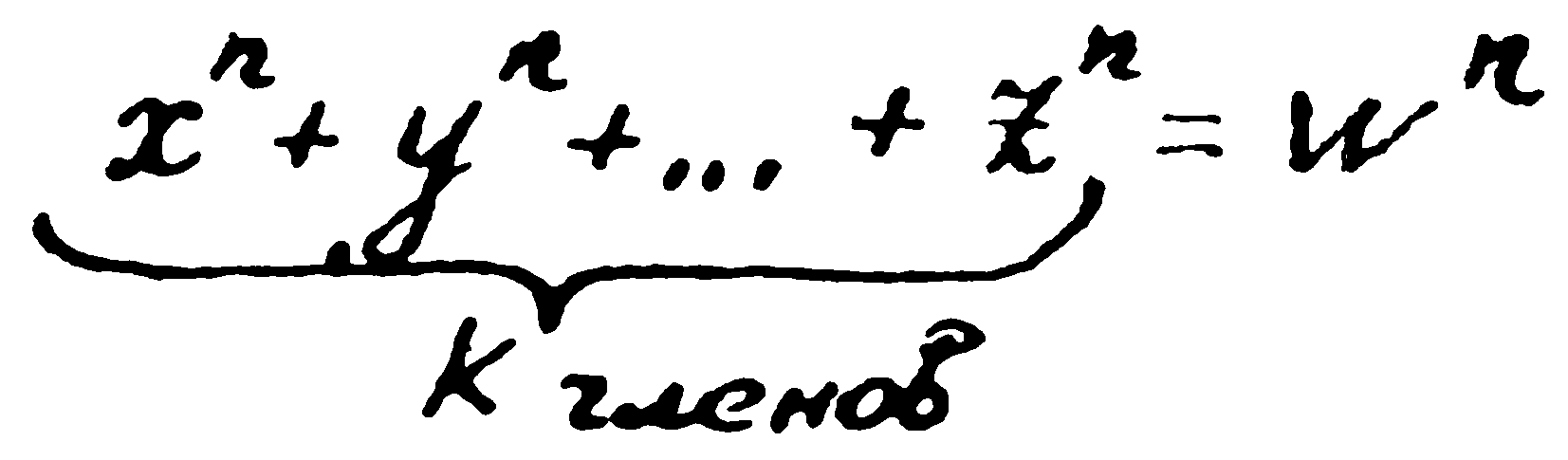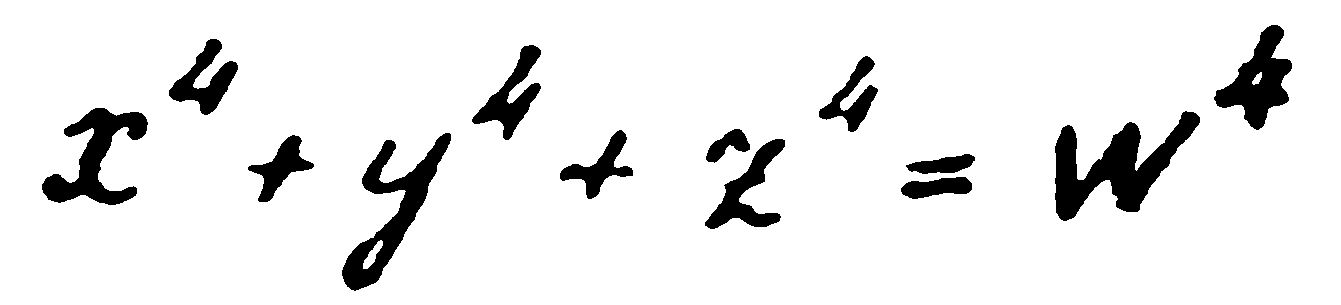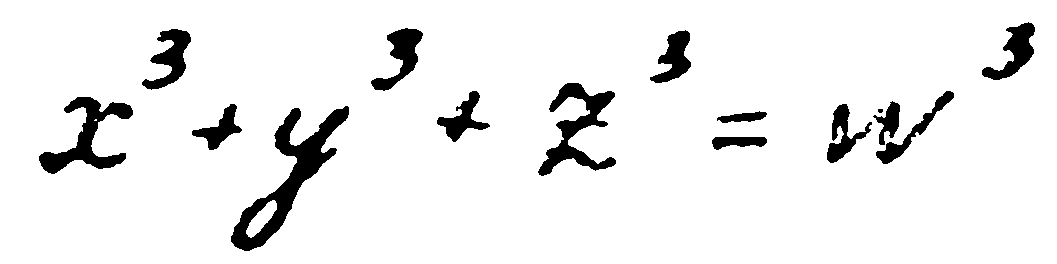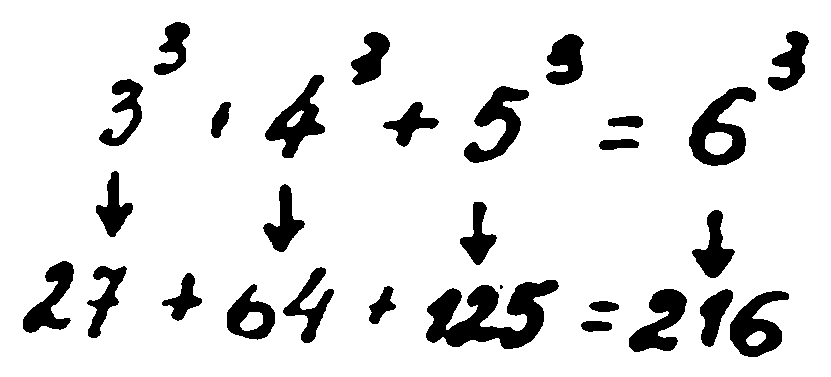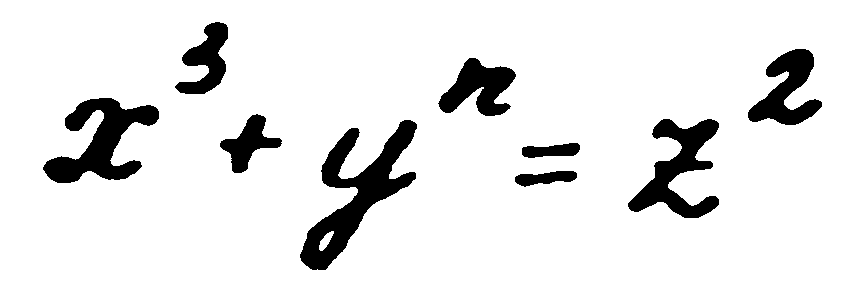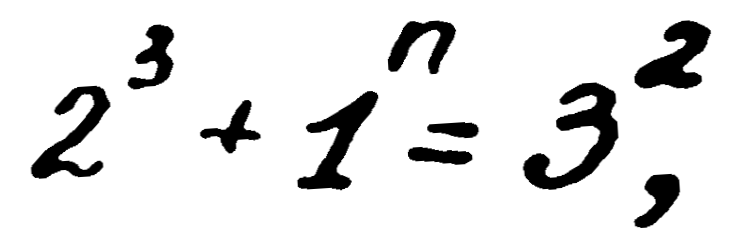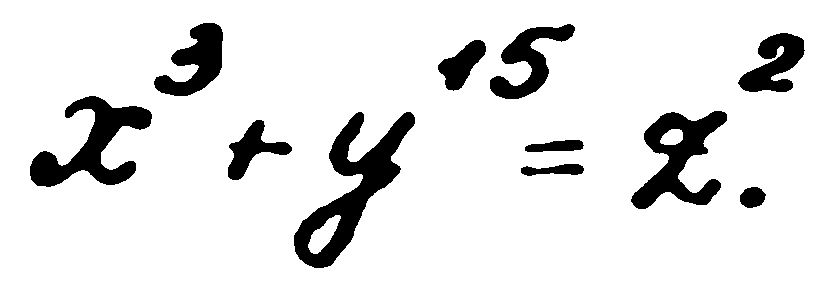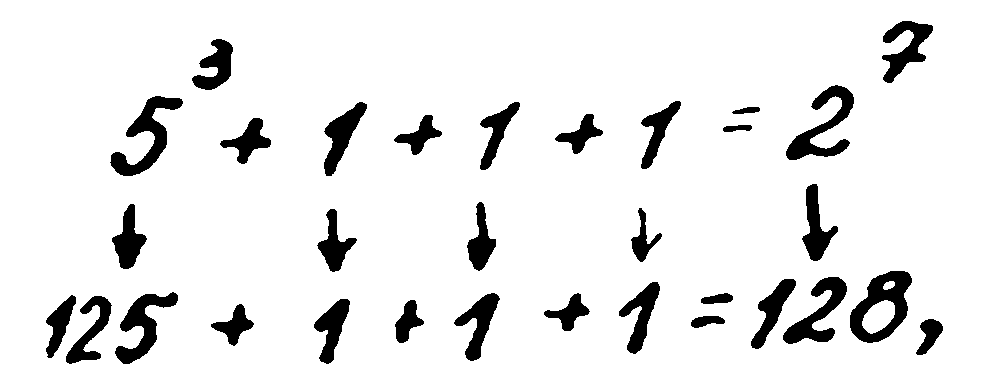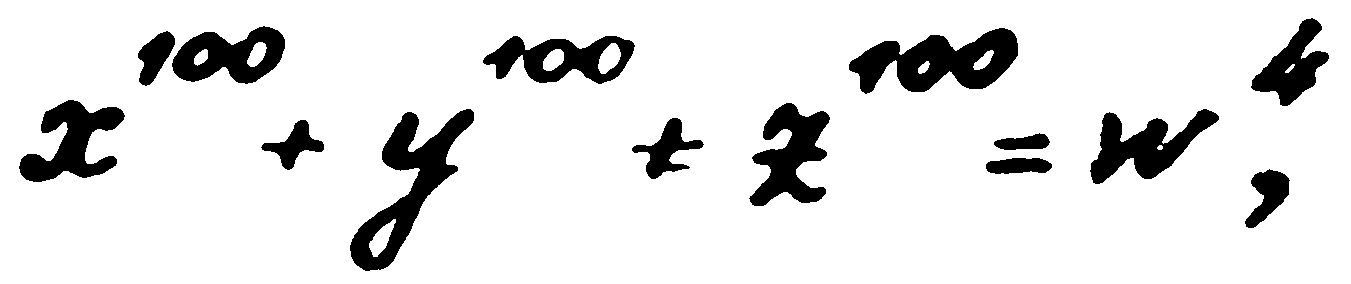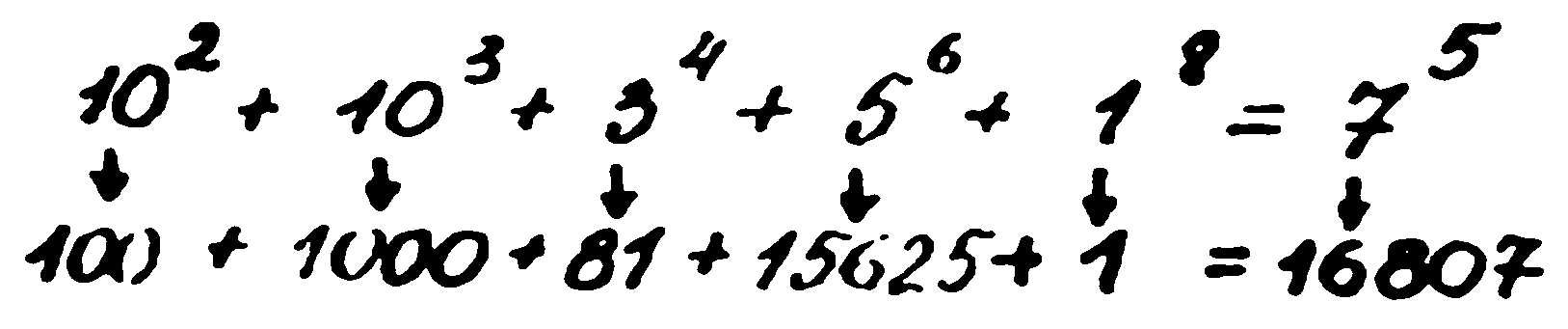Владимир Юровицки
Диофантов кинжал

Когато се запознах с доктор Уотсън, той беше вече много стар, самотен, сантиментален и словоохотлив. Както повечето хора на неговата възраст, обичаше да си спомня далечното минало, а аз с интерес слушах разказите му, посветени най-вече на знаменития Шерлок Холмс.

По-голямата част от чутото ми бе известно от публикациите на някой си Конан Дойл, когото старецът явно не харесваше, въпреки че му признаваше живост на перото.

По онова време Уотсън живееше в графството Чериуъшър. Малкият му дом бе ограден от обширни пространства обрасли с хвойнови храсталаци — любимо място за разходките ни. Бастунът на доктора ровеше в хвойната, а самият той размотаваше дългата нишка на спомените си. Може би някога ще разкажа на читателите някои нови истории за великия детектив, но сега ми се иска да ви доверя една от тях, която оказа съществено влияние върху собствената ми съдба.

— Кажете, сър — попитах веднъж, — как Шерлок Холмс завърши дните си? Нима той просто е остарял и е умрял, като обикновен смъртен?

Уотсън потъна в дълбоко мълчание, което не се осмелявах да прекъсна. Накрая, като че ли се отърси от нещо, стана и тръгна направо през полето. Аз го следвах. Когато спря, видях ниско хълмче, върху което лежеше плоча. На нея бе издълбан надпис: „ШЕРЛОК ДАЙРЕЙТИ ХОЛМС“. По-нататък следваха ред цифри. Те изиграха такава роля в цялата тази история и в моя живот, че ги запомних завинаги.

Уотсън стоя дълго с наведена глава, след това посочи плочата и тихо каза:

— Тук почива моят приятел, а цифрите са автографът на убиеца.

— Как? — възкликнах аз. — Шерлок Холмс е бил убит? Но кой е убиецът? Не го ли настигна ръката на правосъдието?

— Настигна го десницата на наказанието и това бе ръката на самия Холмс.

— Извинете, сър, но как е възможно? Убиецът да бъде убит от собствената си жертва?

— И все пак е така Мистър Холмс бе погубен от злодея, когото сам унищожи десет години преди собствената си смърт.

— Но кой е този убиец?

— Професор Мориарти.

— Професор Мориарти, който загина при схватката край Райхенбахския водопад? Необяснимо! А какво означават цифрите върху камъка?

— Това е кинжалът, Диофантовият кинжал, който убиецът заби в гърдите на моя приятел. Кой друг би могъл да измисли толкова жестоко мъчение освен този велик злодей?

— Но защо тези цифри да са Диофантов кинжал, както благоволихте да се изразите…

— Това е израз на самия Холмс.

— А защо са върху неговия гроб?

— Хайде, млади човече, да отидем в къщи. Там ще ви разкажа тази история с всичките й подробности.

Седнахме пред камината. Думите на стареца се лееха в полумрака. Тази обстановка и сутрешното посещение на гроба на Холмс придаваха на чутото материалност и достоверност. Затова чувам и днес всяка дума, с всички интонации на старческия глас.

— В края на 19.. година бях принуден да напусна Лондон за няколко месеца. По онова време Шерлок Холмс се намираше в зенита на славата си. След като ликвидира бандата на Мориарти, той разкри още редица престъпления, после и няколко тежки съдебни грешки — той се гордееше най-много, когато спасяваше невинния от незаслужени страдания. Преди моето заминаване обаче Холмс се занимаваше с теоретичната криминалистика. По онова време е Лондон бяха станали много модни руските папироси с дълги мундщуци. Както е известно, при пушенето им мундщукът се смачква. Холмс си бе поставил за цел да изследва връзката между начина на смачкването и външния вид на пушача. Размерите на хлътванията върху мундщука, говореше Холмс, съответствуват на размерите на пръстите, а последните сравнително точно корелират с ръста и телосложението на човека. Сдъвканият мундщук пък красноречиво свидетелствува за психичното състояние на пушача и така нататък.

Да си призная, аз скептично се отнасях към новото увлечение на стария си приятел. През цялото време Холмс или бродеше из Лондон и събираше смачкани угарки, или седеше на Бейкър стрийт и ги изследваше под микроскопа. Целият апартамент бе буквално затрупан с угарки, които излъчваха чудовищно зловоние и предизвикваха мълчаливото възмущение на нашата мила хазайка. Но Холмс бе така увлечен в своите занимания, че не забелязваше мишо. Когато заминавах, бях убеден, че заниманията с угарките ще отнемат на Холмс няколко години — той вършеше всичко солидно. Но когато се върнах на Бейкър стрийт, заварих пълна смяна на декорацията.

Угарките и микроскопите бяха изчезнали, а цялата стая на Холмс бе затрупана от… цифри. Върху масата, върху дивана, по креслата, прозорците и шкафовете, навсякъде лежаха листове, изписани с цифри, цифри, цифри… Любопитството ми бе раздразнено, но не се издадох, защото знаех, че Холмс ще ми разкаже всичко сам. Така и стана.

След няколко дни, при поредното ми посещение, той се откъсна от изчисленията си, седна в креслото и започна:

— Скъпи Уотсън, чувствувам, че изгаряте от любопитство. Сега ще ви разкажа някои работи, но ви предупреждавам, че това дело е свръхсекретно. Спомняте ли си още за професор Мориарти?

— Боже мой, как да не си спомням? Спомените за тези две ужасни години, които прекарах, оплаквайки вашата смърт, и сега ме карат да потръпвам. Но какво е могло да се случи с него? Нима и той е възкръснал от мъртвите както вие навремето?

— Не, не, успокойте се. Не е възкръснал, поне не физически. Въпреки това делото му все още не е завършено. Професор Мориарти оглавяваше цял престъпен синдикат. Но действителността надхвърли всичките ни представи. Не без известна помощ от страна на вашия покорен слуга бяха изяснени истинските размери на тази престъпна организация. В много страни полицията арестува участниците в тази най-голяма за цялата история на цивилизования свят банда.

Но не това ни интересува сега. Скотланд ярд успя да открие в една съвсем необикновена къща край Лондон тайната главна квартира на Мориарти. При обиска намериха таен сейф, зазидан в стената.

В него сред различните уличаващи материали, благодарение на които успяха да установят истинските размери на тайната организация и да й нанесат съкрушителен удар, имаше и една малка зелена папка. Когато я разтвориха, агентите на Скотланд ярд едва не получиха удар. В нея се намираше опис на съкровището, което организацията бе заграбила и натрупала през десетилетното си съществуване. Съкровището бе наистина огромно. Тук бе знаменитият рубин Так Хо с тегло 1213 карата, изчезнал при превземането на Кохинхина от французите, брилянтът Шахур от съкровищницата на Тамерлан и множество по-малки знаменити, но също така изключително скъпи камъни: изумруди, сапфири, огромни аметисти. В описа има златни фараонски маски, украшения от скъпоценни камъни, но най-ценното бяха повече от сто неизвестни на науката папируси. Трудно е дори да си представим какво значение за историците би имало прочитането им.

В съкровищницата на Мориарти се намират уникални предмети от цивилизацията на инките и ацтеките, безценни творения на майсторите от италианското Възраждане — например смятаната за безвъзвратно изчезнала картина на да Винчи „Портрет на мона Лутия сред люляците“. Там има и творби, излезли под четката на Рафаело, Джорджоне, Ван Дайк, някои откраднати от Лувъра, Прадо, Ватикана, Дрезден и други, смятани за унищожени.

На вас, естествено, ви се върти на езика въпросът: открити ли са тези съкровища? И сега започва следващото действие на драмата. Установи се, че местонаходището на съкровището са знаели само професорът и трима негови най-доверени съучастници. По-скоро случайно, отколкото предумишлено, но тримата съучастници на професора бяха убити, а самият той загина в известната схватка. Така че днес никой не знае къде се намира съкровището.

Въпреки всичко в началото никой не се обезкуражаваше. Работата бе, че в края на описа с ръката на самия професор бе написано: „Местонаходището на съкровището…“

И Холмс ми подаде картичка, върху която бе изобразено следното:

— Това е шифър — казах аз.

— Отгатнахте, Уотсън, това наистина е шифър. И в края на краищата няма такъв шифър, който да не може да бъде разгадан.

Срочно бяха мобилизирани най-големите специалисти от Скотланд ярд и други служби за дешифриране. По-нататък към работата внимателно били включени специалисти от САЩ, Франция и дори от Генералния щаб на Русия, но, уви, всичко беше напразно. Дешифраторите като един заявиха, че е била използувана напълно неизвестна система и техните методи са безсилни.

Тогава привлякоха такива изявени математици като Хамилтън, Поанкаре, Чатандрагар, но и те не можаха да помогнат. Лично министър-председателят се обърна към мен с молба да взема участие в това дело.

— И вие се съгласихте?

— Не без известни колебания. Честно казано, бях малко обиден, че Скотланд ярд се бе опитал да ме изолира от разследването въпреки ролята ми в разгромяването на организацията на Мориарти. Но не можех да откажа на министър-председателя. А и не ми се искаше. Първо, обичам костеливите орехи, а този по всяка вероятност бе един от най-костеливите. И второ, в схватката при водопада лично аз унищожих главния свидетел и мой морален дълг бе да направя всичко, за да върна на човечеството усмивката на мона Лутия.

— И вие се надявате, че ще успеете, Холмс?

— Надявам се. Много съм се занимавал с проблемите на шифрите, спомнете си само танцуващите човечета.

— Да, но сега? Намерихте ли ключа към този шифър?

— Уви, скъпи Уотсън, очевидно съм още далеч от него. Но все пак има известни проблясъци.

С това завърши нашият първи разговор.

* * *

След две седмици, през които Холмс не излизаше от жилището си на Бейкър стрийт, цял потънал в изчисления, ние отново се върнахме към тайната на шифъра.

— И така, Уотсън, нека внимателно разгледаме шифрираното. Виждаме, че то се състои от цифри, които са обединени в шест блока или матрици, обградени с малки скоби. Блоковете съдържат различен брой редове и колони, разположени са линейно и с вертикална черта са разделени на два суперблока.

Да погледнем на тази записка като на някакъв вид писменост. В теорията на писмеността се разглеждат следните видове:

1. Идиоматично писмо.

2. Йероглифно писмо.

3. Сричково писмо.

4. Буквено писмо.

В идиоматичното писмо отделната единица изразява цели фрази, често напълно завършени по смисъл. Пример за идиоматично писмо е любителският радиокод, при който „К“ означава край на предаването. Друго такова писмо са математическите символи. Точката означава, че двете числа трябва да се умножат, т.е. цяла завършена мисъл. Знакът плюс — че стоящите до него числа трябва да се съберат и т.н. Дори в обикновеното ни писмо, което приемаме за буквено, има идиоматични елементи — това са препинателните знаци.

В йероглифното писмо всеки знак означава дума. Това е най-древният вид писменост. Но и до днес тя се използува върху почти една трета от земното кълбо.

В сричковото писмо всеки знак означава отделна сричка или някоя устойчива звукова група. Сричковите системи в чист вид отдавна са измрели, макар че останки от този вид писменост са се запазили в някои езици. Но не вярвам Мориарти да е използувал сричкова система. Тя е толкова архаична, че само специалисти по археолингвистика биха могли да се оправят в подобна работа. Затова ще я изключим от по-нататъшния анализ.

И накрая — върхът на творческия гений на Човека: буквеното писмо, което оптимално преобразува звуковата информация в зрителна.

Следователно първият въпрос е: какъв тип писменост е тази шифровка? Очевидно, че единицата от тази писменост, нейният знак, е цифровият блок. Ако писмото е идиоматично, то всеки блок представлява отделна фраза. Имаме всичко шест фрази. Предполагам, Уотсън, че за да се шифрира местонахождението на съкровището, това е твърде много. Фразите са разделени от отвесни черти на две групи, първата съдържа една фраза, а втората — пет. Фактически се получават два абзаца или ако искате, две строфи. Но нали това не е стихотворение, за да се разбива на толкова едри семантични единици. Значи можем напълно обосновано да заключим, че това не е идиоматично писмо.

Да предположим, че даденото писмо е йероглифно, тоест всеки блок е символ, знак, йероглиф на някоя дума. Тогава разделянето с отвесна черта натрапва предположението, че имаме текст от две фрази, едната от една, а втората — от пет думи. Разбира се, съществуват изречения от една дума. Те са присъщи на устната реч, но те повече повишават изразителността, а не информативността й. Това са междуметия от типа „да“, „не“, и пр. Затова основанията ни са достатъчно сериозни, да отхвърлим и тази хипотеза.

По този начин остава последният вариант. Даденото писмо е буквено, а отделният цифров блок е буквен знак. Тогава съобщението се състои от две думи, от които първата може да бъде само предлог, понеже е еднобуквена и стои на първо място. Има само два еднобуквени предлога за място и направление: предлозите „в“ и „у“. Така че разпознахме едната буква с алтернативна точност. Втората дума съдържа пет букви.

— Наистина, Холмс, всичко изглежда ужасно убедително. Ако и Мориарти е разсъждавал така, би било чудесно.

— Предполагам, че Мориарти въобще не се е замислял над този въпрос. Той е шифровал като обикновен нормален човек, превеждайки чисто автоматично усвоената от детство писменост на друга система за записване. Но едва сега ние имаме основания за такова съждение.

— Добре, Холмс, но сега навярно работата ще тръгне значително по-бързо. Помня, че в делото с танцуващите човечета вие приложихте честотния анализ, за да откриете шифъра. Мисля, че този метод може да се приложи и тук.

— Наистина честотният анализ е най-мощното оръжие в ръцете на дешифриращия. Преброявате колко пъти се среща всеки знак, делите това число на обшия брой знаци в съобщението и получавате честотата на всеки знак. Честотните спектри на всички основни езици са много добре изучени, издадени са и специални таблици. Нещо повече, има не само таблици за честотата на отделните знаци, но и такива на два знака заедно. Така се извършва дешифрирането на буквеното писмо. Но спомнете си, Уотсън, колко знаци имах тогава на разположение.

— Не по-малко от сто.

— Ето къде е въпросът. Сега имам само шест знака. При това нито един не се повтаря. Тук честотният анализ е безсилен.

— Тогава какво ще правите, Холмс?

— Този въпрос непрекъснато си задавам и аз. Още не ни е известна системата на шифриране. Как, на какъв принцип една или друга буква се свързва с цифровия блок? Трябва да поработя още.

Така завърши вторият ни разговор.

* * *

Третият се състоя буквално след няколко дни. Холмс започна без предисловие:

— Кажете, Уотсън, бихте ли могли да запаметите повече от тридесет ето такива таблици? — И той написа:

— Естествено, че не.

— Така си и мислех. Впрочем не става дума за обема на паметта на Мориарти.

Нека си припомним, че Мориарти беше учен, той твърдеше, че е завършил някъде си университет, и от личния си контакт с него аз напълно вярвам, че е така. Би ли могъл тогава той да е толкова глупав и алогичен, та да измисля собствена писменост от таблици-азбука и по тоя тъп начин да шифрова с нея? Не. Аз отговарям, не! Логиката на учения не го допуска. Самият стил на европейската наука изисква от минимум данни да се получава максимум информация. Освен това би трябвало някъде да съхранява ключа на тази писменост, защото явно не е възможно да наизусти подобна азбука… Следователно ще съществува твърде голяма вероятност или някой да разкрие шифъра, или просто да загуби ключа. Мориарти беше твърде умен, за да не го разбере. И какво следва от всичко това, Уотсън?

— Според мен абсолютно нищо освен онова, което вече казахте, Холмс.

— Много, твърде много, мили докторе. Това означава, че всяка структурна единица, всеки цифров блок не е просто безсмислен набор от цифри, а напълно закономерен и подреден. Нима това не е откритие?

— Извинете, Холмс, но аз не виждам тук никакво откритие.

— Ах, Уотсън, Уотсън, за вас, медиците, логиката на цифрите е недостъпна. Нима не е ясно, че е безсмислено да се опитваш да разшифроваш текст, ако всеки елемент е случаен, ключът е изгубен, а статистика няма. Но ако елементите на шифъра се подчиняват на вътрешни закони, то задачата вече не е така безнадеждна.

Нека още веднъж разгледаме цифровите блокове. Да разгледаме редовете. В един блокове те са абсолютно идентични, в други се променят след първия елемент. Сега да видим колонките. Всички започват от едно и също ниво и нямат прекъсвания. Няма две напълно еднакви колони. Това е вече система. Докато при редовете цари пълен хаос. Сега ясно ли ви е?

— Уви, не.

— Но как не разбирате? Та това сочи, че именно колоните образуват информационната подструктура на блоковете, а не редовете. Че колонката съхранява няколко кванта информация, а съвкупността от тези кванти дава информацията за буквата. Сега ясно ли ви е, Уотсън? Всеки блок трябва да се чете по колонки, а не по редове.

— Сега ми е ясно. Но по-нататък?

— Нямам абсолютно никаква представа. Но ще размислим. Ще мислим над колонките. Защо са различни по дължина, защо са различни по количество? Над това вече има за какво да се помисли, Уотсън.

* * *

През следващите няколко месеца срещах Холмс само случайно. Той вечно бързаше за някъде. Непрекъснато отсъствуваше от къщи. Не знаех какво го кара да скита из покрайнините на Лондон и дори в доста отдалечени градове. Но чувствувах, че това е свързано със загадката Мориарти.

— Уотсън, можете да смятате, че мона Лутия вече виси на тая стена.

— Как, Холмс, вие сте разчели шифъра на Мориарти? Поздравявам ви…

— Почакайте, Уотсън, не съм стигнал още до там, но ключът от шифъра е в ръцете ми. Вижте — и той пак извади картончето с шифъра. — Какво установихме миналия път? Че всеки цифров блок трябва да се чете отвесно, по колони. Виждаме, че тук има букви, които съдържат една, две, три или четири колони, т.е. от един до четири дадени елемента. Що за код ще е този, при който буквите могат да се шифрират с помощта на последователности от един до четири елемента?

— Честно казано, Холмс, не знам.

— Кодът на Морз. Това е морзовата азбука! Вие разбирате ли, тривиалната морзова азбука, която всяка колона шифрира или точка, или тире, а последователността на тези точки и тирета дава кода на буквите. Всичко е ужасно просто, Уотсън. Тези няколко месеца аз се заех да изуча някои обстоятелства от живота на Мориарти в Лондон. И успях да открия нещо изключително важно. В живота на професора е имало период, когато той е трябвало да се крие от собствените си съучастници, понеже в организацията започнала борба за власт. В края на краищата победил Мориарти. Но няколко месеца е трябвало да се крие. И аз установих, че тогава е работил на гарата на Бирмингамската железопътна линия като обикновен телеграфист. Там и досега използуват телеграфни апарати по системата на Морз. Това е много важно за нас, защото сега кодът на Морз в телеграфията навсякъде е изместен от кода на Бодо. А ако Мориарти беше използувал кода на Бодо, нашите успехи биха станали твърде проблематични. В радиотелеграфията, особено при радиолюбителите, той и досега си остава основен. Кодът на Морз се състои от последователни импулси, всеки от които бива точка или тире. Броят на импулсите в различните букви е различен — от един до пет. Точно по това се отличава морзовият код от кода на Бодо, в който всички букви имат по пет импулса. Ще ви напиша морзовата азбука, за да ви е по-лесно да следите мисълта ми.

По един импулс имат две букви. Четири имат по два, осем — по три, и шестнадесет — по четири импулса. Един импулс е една колонка в блока. Имаме един едноколонков блок, един двуколонен, два триколонни и два четириколонни. Сега да разгледаме по-внимателно шифъра. Вече с голяма вероятност приехме, че първата буква е „у“ или „в“. Вероятно последният блок е окончание. Той е едноколонен, при един импулс това може да бъде или буква „е“ или „т“. Щом е окончание, по-вероятно е да означава „е“, отколкото „т“, например „в дороге“^[1], а не с предлога „у“. Виждаме обаче, че в морзовата азбука буквата „в“ е триимпулсна, а и в шифъра първата буква е триколонна. Следователно имаме пълно съвпадение. По този начин определяме първата буква като „в“, а последната — „е“. Виждате, че доста напреднахме. Вече знаем две букви от шифъра. Нещо повече — установихме, че колоните

означават точка, а колоните

означават тире.

— Да, Холмс, виждам че не сте си губили напразно времето и вече сте близо до целта. Но можете ли да кажете какво означават останалите тринадесет колони?

— Да, мога. Или точка, или тире. Но още не мога да различа точката от тирето. Структурата на колонките ми е съвършено неясна. По какъв принцип тройката числа 3, 15, 2 се отнася към класа точки, а тройката 4, 4, 4 — към класа тирета, още е загадка за мене. Очевидно Мориарти е приложил някакво правило, с което произволна последователност от натурални числа може да се отнесе към единия или към другия клас. Изразено на чисто математически език, той е разчленил някакво множество от натурални числа на две непресичащи се множества и всяка последователност от едното подмножество означава точка, а от другото — тире. Но ние вече познаваме четири образеца на това разчленяване и аз съм почти сигурен, че откриването на решаващото условие няма да представлява особена трудност. Така че, Уотсън, пригответе стената да приеме мона Лутия.

* * *

Петият ни разговор се състоя след една или две седмици. Холмс беше толкова възбуден, че това просто не съответствуваше на стила му на вечно сдържан джентълмен.

— Уотсън, струва ми се, че в съзнанието ми се е появила ужасна мисъл. Защо 2–2–2 е да, а 4–4–4 е не (да — точка, а не — тире)? Вчера разглеждах на закуска сутрешния вестник. По-късно ще ви кажа какво пишеше там и си помислих, че тези двойки и четворки могат да се запишат във вида:

Разбирате ли, Уотсън, какво означава това?

— Разбира се. Все пак в колежа съм учил математика. Хикс, игрек и зет са някакви числа и когато се повдигнат на втора или на четвърта степен, се получават равенства.

— Всичко това е вярно, Уотсън, само че числата хикс, игрек и зет могат да бъдат само цели, натурални — 1, 2, 5, 100 000, но не 1,1 или 0,95. И още едно „но“. Впрочем чували ли сте за Пиер Ферма?

— За съжаление никога.

— Тогава седнете в креслото и чуйте една от най-детективските истории в математиката. През XVII век във Франция е живял юристът Пиер Ферма. Обаче истинската му страст била математиката и особено теорията на числата — раздел, занимаващ се със свойствата на натуралните числа. На Пиер Ферма принадлежат редица първокласни резултати. Той например доказал много важната Малка теорема на Ферма. Но най-голямата известност сред широката публика е получила теоремата, която математиците, хора достатъчно трезви, са нарекли тържествено Великата теорема на Ферма. Известно е, че можем да съберем два квадрата и да получим квадрата на трето число. Това са знаели още египтяните. Например числата 3, 4 и 5 се наричат египетски, понеже

Казано на математически език, равенството

е решимо в целите числа.

А ако сега вземем трета, а не втора степен? Могат ли да се намерят две такива числа, които, повдигнати на трета степен и после събрани, да дават куба на трето число? И ако такива числа не съществуват за n=3, то при какви стойности на n съществуват такива числа? Така е възникнал проблемът: при какви стойности на n равенството

допуска решение в цели числа.

Пиер Ферма заявил, че при каквото и да е n, освен 1 и 2, равенството е невъзможно в цели числа. Нещо повече, той твърди, че е доказал това нещо строго математично.

Опитите на мнозина математици да повторят доказателството или да намерят ново оставали напразни. След смъртта на Ферма в книжата му намерили само забележки по полетата на математическите книги, в които се дава формулировката на теоремата „за нерешимостта“, и след това е написано: „Доказателството е твърде дълго, за да се приведе тук.“ Нищо повече, нито ред на тази тема. Така досега не се знае дали Ферма наистина е доказал Великата теорема.

Позволявам си да изкажа собственото си мнение по този въпрос. Вие знаете, че макар и да не съм професионален математик, винаги съм бил любител на тази наука, защото моят дедуктивен метод изисква задълбочен математически стил на мислене. И си позволявам да мисля, че Ферма е доказал теоремата. Работата е в това, че тя е била съвършено необикновена за XVII век. По онова време математиците са решавали задачите, а не са доказвали тяхната нерешимост. Те са търсели корените на алгебричните уравнения от произволна степен, опитвали са се да разделят ъгъл на три части само с помощта на пергел и линия; да построят квадрат с повърхност, равна на повърхността на даден кръг; опитвали са се да докажат Петия постулат на Евклид. Едва през XIX век бе доказано, че тези задачи са нерешими.

Впрочем, Уотсън, като че ли се увлякох. И така, да продължим. От XVII век тази теорема предизвиква математическия разум. Било проверено, че при n, по-малко от 2047, уравнението на Ферма е нерешимо в цели числа. Но това не е отговор на задачата. Възможно е при n, равно на 100 милиона, да съществува решение.

Нов стимул за щурмуването на Великата теорема на Ферма бе сумата от един милион марки, която един немски индустриалец завеща на онзи, който я докаже. За работа се заловиха домакини и ученици, портиери, учители, шивачи, моряци. Гьотингенският университет, който трябваше да присъди тази награда, бе затрупан от „доказателства“. Уви, както трябваше и да се очаква, всички те се оказали неверни.

Вестникът, за който обещах да ви разкажа, съобщаваше, че един японски ученик е доказал Великата теорема и математици от Токийския университет не могат да намерят грешка в доказателството му. По всяка вероятност това е поредната журналистическа сензация. Но когато четях съобщението, ме прониза една мисъл. Не е ли използувал Мориарти Великата теорема на Ферма за своя шифър? Защото ако последователността 2–2–2 се запише във вида

това ще означава, че даденото уравнение е решимо в цели числа и следователно, принадлежи към класа на решимите уравнения на Ферма. Ние можем да отнесем и самата последователност в специален клас. Същевременно, ако вземем последователността 4–4–4 и я запишем във вида

то това уравнение е нерешима в цели числа, както го доказа още великият Ойлер. Затова и последователността 4–4–4 трябва да отнесем към друг клас. В конкретния случай имаме последователности от различни класове. От друга страна, знаем, че първата последователност означава точка, а втората — тире, ако първият блок действително означава буквата „в“.

— Наистина, Холмс, всичко това е ужасно интересно и смело. Но уверен ли сте, че е вярно?

— За съжаление моето предположение трудно може да се потвърди. Защото само първите две колони подхождат на уравненията на Ферма. В останалите случаи или броят на членовете на уравнението е повече от три, или степенните показатели не са еднакви. И все пак, Уотсън, интуитивно чувствувам, че се намирам съвсем близко до ключа на шифъра. Нещо повече, на времето до мен стигна слухът, че Мориарти е бил математик. Така че проблематиката на Великата теорема му е била позната.

— Още веднъж ще ви кажа, че ужасно искам да сте прав.

С това нашият пети разговор завърши.

* * *

Шестият, както обикновено, започна с въпрос на Холмс.

— Уотсън, знаете ли, кой е Диофант?

— По всяка вероятност грък. Но сред моите познати такъв грък, струва ми се, няма.

— И нищо удивително. Той е живял преди хиляда и петстотин години.

— Боже мой, Холмс, вашите изследвания ви водят към някакви исторически бездни. Беше XVII век, сега пък III. Следващия път ще почнем от потопа и ковчега.

— Уви, докторе, за да разкрия тази загадка, ще се наложи да отидем твърде далеч във времето. И така, този грък Диофант бил забележителен математик, един от първите, описали уравнения, които впоследствие били наречени на негово име. В тези уравнения отговорът може да бъде само в натурални числа. Ето ви най-простото диофантово уравнение: трябва да се разделят пет ябълки на трима души, но така, че всеки да получи поне по една ябълка. Алгебричното решение на това уравнение е просто — на всеки по една ябълка и две трети. Но при Диофант този отговор не е верен, защото при него ябълката не може да се дели. Значи можем да дадем на двама по една ябълка и на третия — три, или на двама по две, а на третия — една. За разлика от обикновената алгебра, при която решението е само едно, в алгебрата на Диофант има няколко решения. В някои случаи и тук може да има само едно решение — например да се разделят пет ябълки на петима души. А може да няма нито едно — да се разделят на шест души.

Сега разбирате, че уравнението на Ферма е също диофантово уравнение, само че от по-висша степен. Но освен уравненията от типа на Ферма и на Ойлер с две събираеми в лявата част, съществуват и по-общи уравнения. Например Ойлер а научавал следния тип:

Той смятал, че тези уравнения не могат да имат диофантови решения при k, по-малко от n или, е други думи, когато броят на събираемите в лявата страна е по-малък от степенния показател на уравнението. Уви, това твърдение е само хипотеза, но все пак изказана от Ойлер — математик с поразителна интуиция, и ние можем да му повярваме.

И така, третото тире в предлога „в“, с който започва текстът, е изобразено с четири четворки и ние можем да го представим като диофантово уравнение.

Съгласно хипотезата на Ойлер то не може да има решение в цели числа. Според моето предположение за кодиране на импулсите това е тире. Още едно потвърждение на хипотезата, че Мориарти е използувал правилото: ако има решение в цели числа, колонката означава точка, а ако няма — означава тире. Да погледнем сега третата буква от шифъра. Тя се състои от две колони, а в морзовата азбука от шестте гласни само две са двуимпулсни. От 26 съгласни също само две са двуимпулсни, но при гласните вероятността е 1/3, а при съгласните — 1/13. Следователно с шанс 80% можем да приемем, че тази буква е гласна. Двуимпулсните гласни са „а“ и „и“. И двете започват с точка, докато съгласните започват с тирета. Първата колонка на тази буква е 3–3–3–3 и според хипотезата ни отговаря на диофантово уравнение от вида

Тук броят на събираемите вляво е равен на степенния показател, т.е. това уравнение има диофантово решение. И наистина

Тогава колонката трябва да означава точка. Което установихме и по друг начин. Сега познаваме две букви с абсолютна точност и една — с алтернативна.

— Отлично върви, Холмс. Но ако все пак сте тръгнали по лъжлив път? Защото в останалите колонки не виждам нито последователност на Ферма, нито на Ойлер. Какво може да означава 2 — 3 — 4 — 6 — 8 — 5 според вашата теория?

— И аз не знам. Затова трябва да узная всичко за Мориарти. Уверен съм, че неговата биография ще ни даде ключа към решаването на тази загадка.

Така завърши шестият ни разговор.

* * *

После Холмс задълго изчезна от мъгливия Албион. Получавах кратки писма от Франция, Италия, Германия. Съобщаваше ми, че научил интересни нови факти. Изминаха две години, преди да го срещна пак.

— Скъпи Холмс — започнах аз, — донесохте ли мона Лутия?

— Това беше наистина успешно пътуване, Уотсън. Напълно се убедих в моя метод за дешифриране на текста. Но успях да открия и нещо, което за първи път ме кара да се замисля дали моята дейност служи за добро. Усъмних се в правотата си, Уотсън.

— Боже мой, Холмс, какво толкова трагично сте могли да узнаете в областта на някакви си диофантови уравнения? Нима в математиката също има трагедии?

— Вие смятате математиката за освободена от човешките страсти? Това е голямо заблуждение. Ето ви за пример историята на един талантлив юноша на име Джакомо Писети. Той се родил в семейството на преподавател по математика в Сицилия. Още дете, проявил изключителни математически способности. На петгодишна възраст открил грешка в изчисленията на баща си. Особено много се интересувал от теорията за числата. И, естествено, не е могъл да отмине Великата теорема на Ферма. Петнадесетгодишен, той доказва, че уравнението

е решимо в цели числа за всяко n. Ходът на разсъжденията му по принцип не е сложен, но е твърде оригинален. Понеже 2 на трета степен е 8, а 3 на втора степен е 9, то може да се напише

Но единица на която и да е степен е пак единица и като изразява равенството във вида

той извел своята теорема.

— Почакайте, Холмс. Без да искам, започнах да се замислям над вашия шифър. И забелязвам, че последната колонка е 3–15–2, т.е. фактически уравнението на младия Джакомо

Но ако то е решимо в цели числа при хикс = 2, игрек = 1 и зет = 3, то тази колонка означава точка.

— Уотсън, никога не съм допускал, че математиката ще увлече и вас. Напълно сте прав. Понеже последната колонка означава буква, то тази буква би трябвало да е „е“, което определихме и по граматически съображения.

— Но какво отношение има младият Джакомо към нашия шифър?

— Ще продължа, Уотсън. Той следвал в Гьотингенския университет при Хилберт и Кумер. Там продължава да работи над Великата теорема. За да улесни пътя си, той разглежда най-напред по-общи уравнения от тези на Ферма и Ойлер, уравнения от типа

с произволни цели значения на степенните показатели и произволен брой членове. Тях той нарекъл нулево-параметрични диофантови уравнения. Лесно е да се види, че уравненията на Ферма и на Ойлер са техни частни случаи. Писети иска да намери критерий за решимостта на произволни нулево-параметрични диофантови уравнения. И се връща към работите си от детството. Още преди бил забелязал, че решения от типа, който намерил някога, дават критерий за решимостта на цял клас нулево-параметрични диофантови уравнения. И щом е вярно, че

от това следва, че уравнението

е решимо в цели числа за произволни n, m и p. Решенията на нулево-параметричните диофантови уравнения, в които поне едно от неизвестните е единица, били наречени решения на Писети. После Джакомо открил, че между решимите диофантови уравнения и решенията на Писети съществува определена връзка. Той доказал, поне му се сторило, че доказал, че всяко решимо нулево-параметрично диофантово уравнение може да се съпостави с някое решение на Писети. После успял да докаже, че уравненията на Ферма при n, по-голямо от 2, не могат да се съпоставят с нито едно от решенията на Писети. Това било победа. Това било триумф. Представяте ли си как се е чувствувал младежът, когато победил тристагодишната крепост?

Доказателството било проверено и лично от Хилберт, който го изпратил в списание „Анали на математиката“. Но когато статията вече била набрана, най-добрия приятел на Писети, млад математик от Русия, открил грешка в доказателството. Списанието спрели, а великият Хилберт излязъл от кожата си при мисълта, че за малко не станал за посмешище. А Джакомо? Той изпитал толкова силно душевно сътресение, че се наложила психиатрична помощ. От болницата излязъл блед, слаб и озлобен срещу целия свят. В математическите среди не чули нищо повече за Джакомо Писети.

— Искате да кажете, Холмс, че затова пък се появил професор Мориарти?

— Да, Уотсън. Писети умрял, но се родил злодеят професор Мориарти.

— Как е станало това превъплъщение?

— Има твърде много тайни в тази история. Не забравяйте, че Писети е от Сицилия. Установих, че дядо му е бил един от шефовете на тамошната мафия.

— Прав сте, Холмс. Това е ужасна трагедия, Великата теорема на Ферма обърква живота на един талантлив младеж и го довежда до гибел при Райхенбахския водопад. Но хвърля ли това някаква светлина върху шифъра?

— В известна степен, да. Може би сам сте забелязал, че в шифъра е използувано детското уравнение на Писети. Случайността тук е немислима.

Сега съвсем точно познаваме системата за дешифриране. Взема се една колонка, например първата от четвъртата буква — 100–100–100–4, и по нея се съставя нулево-параметрично диофантово уравнение.

Ако то има решение в цели числа, означава точка. Ако няма, означава тире. Като извършим тази операция с всички колони, ще получим буквите по кода на Морз. А щом определим всички букви, ще открием къде се намира съкровището.

— И вие сте направили това?

— Уви, Уотсън, тук се крие тайната. Всички математици, към които се обърнах в Гьотинген, Оксфорд и Сорбоната, в един глас твърдят, че съвременната математика не е в състояние да разреши проблема за тези диофантови уравнения, които им дадох, базирайки се на шифъра. Аз се надявах, че решенията им ще могат да се намерят чрез просто опитване на възможните варианти. Но излезе, че само за горното уравнение, ако вземем дори най-малкото число — две на степен 100, то ще има 30 знака и никакво опитване на вариантите не е възможно не само ръчно, но дори с помощта на появилите се напоследък механични изчислители. Да, ние знаем всичко за шифъра и все пак сме безсилни.

— Но нали Мориарти… по-точно Писети, е шифровал по някакъв начин. Той сигурно е знаел кои уравнения са решими и кои не.

— Сега стигаме до най-загадъчната част на историята, Уотсън. В разговорите си с математиците стигнах до заключението, че това шифриране е възможно само ако човек познава условията за решимост на произволни, подчертавам, на произволни нулево-параметрични диофантови уравнения. Следователно като минимум е необходимо доказателството на Великата теорема на Ферма.

— Ако правилно съм ви разбрал, Мориарти, по-точно Писети, я е доказал?

— Да, Уотсън. Този шифър го доказва с абсолютна сигурност. Той е доказал и Великата теорема на Ферма, и хипотезата на Ойлер, и дори е намерил условията за решаване на всички нулево-параметрични диофантови уравнения.

— Господи… Това означава… това означава, че Мориарти или Писети наистина е бил един от най-големите математици на всички времена… И най-големият злодей. Тук има от какво да се побърка човек, Холмс. И въпреки всичко няма ли някаква грешка?

— Не може да има грешка. Работата е, че той е решавал съвсем друга задача, а не онази, с която са се занимавали всички. Може да се спори дали е вярна или не Великата теорема на Ферма, но верността й не зависи от това. А ако се изведат условията за решаване на произволно нулево-параметрично диофантово уравнение, грешката може да се открие съвсем тривиално. Не забравяйте колко жестоко е заплатил на времето си Писети за една своя грешка. Да допуснем, че той може да я повтори, е немислимо. Психологически немислимо.

— Наистина мога само да повторя, че има от какво да се побърка човек.

— Да, тази картина често се появява напоследък в съзнанието ми. Поруган и осмян, Писети потъва в бездната на престъпния свят, за да отмъсти на хората за своя позор. Той измисля и осъществява най-дръзките престъпни акции. За него миналото не съществува. Той не иска да си го спомня. Но юношеските мечти за Великата теорема на Ферма го преследват. Той се опитва напразно. Но в един момент на тази отчаяна схватка на миналото с бъдещето идва озарението. Блясва светлина и той вижда всичко. Какво е изпитал тогава? Само перото на Шекспир или на Достоевски би могло да го опише. А аз съм само детектив. А после, когато се успокоил, разбрал, че никой няма да узнае за неговото откритие. За него вече няма път назад в нашия свят, включително и в света на науката. Той не би могъл да обяви своето доказателство, без да разкрие себе си. Под каквото и име да го публикува, колегите му биха разбрали, че това е Писети.

И тогава решил да създаде своя награда за онзи, които успее да извърви същия път, а същевременно да запази приоритета си. Наградата ще бъде феноменална. И той усърдно продължава да ръководи организацията си, която краде, граби, трупа безценни съкровища за онзи, който ще дешифрира надписа, ще реши отново задачата, която е решил той.

И тази схватка при Райхенбахския водопад. Тя е пред очите ми. Кого блъснах в бездната — великия злодей или гениалния математик?

— Но, Холмс, вие изобщо не сте имали избор. Или вие, или той.

— А нима това не е избор? Колкото и да се оправдавам, остава фактът: аз убих най-големия математик в историята.

— И злодей.

— Не, математик. Та нали Писети…

— Мориарти, Холмс.

— Нека е Писети — Мориарти… Но аз, Уотсън, чувствувам, че това, което узнах, промени нещо в душата ми. Усещам, че детективът в мен умря. Да раздавам правосъдие, дори да помагам за неговото прилагане, трябва да имам абсолютната увереност, че понятията ми за добро и за зло са непротиворечиви и еднозначни, че те не биха могли от своя страна да станат източник на зло. А сега аз не съм така уверен както преди.

— И какво се каните да сторите?

— Длъжен съм да сторя всичко, за да върна на човечеството тези съкровища и същевременно поне отчасти да възстановя истината за Писети — Мориарти.

— Но вие не сте математик, Холмс. Щом професионалните математици са безсилни, какво бихте могли да направите вие?

— Правилно, Уотсън, аз не съм математик. Обаче Писети е намерил правилния път. А да се върви по него, когато знаеш, че целта съществува, е хиляди пъти по-лесно.

Има и друг начин за разгадаване на шифъра. За да се разпознае тирето, трябва да се направи същото, което е направил Писети. Но за да се дешифрира точката, е достатъчно да се намери поне едно частно решение на съответното диофантово уравнение. И това може да стане по пътя на тъпото опитване на възможните варианти. И ако по този начин мога да открия няколко знака точки, използувайки граматичните правила и кода на Морз, ще мога да намеря приемливо количество варианти на текста. Но тук е нужен късмет, Уотсън.

С това завърши седмият ни разговор.

* * *

После имахме и други разговори, но те вече не представляват интерес. Остава ми само да съобщя епилога. Шерлок Холмс напълно се откъсна от криминалистиката. Остана незавършена дори монографията му за угарките. Занимаваше се само с теорията на числата. В минути на отчаяние горчиво се оплакваше, че Писети-Мориарти е забил диофантовия си кинжал именно в него.

С тъга следях угасването на този толкова мощен някога интелект, който сега изнемогваше от безкрайните изчисления, от непрекъснати математически операции, за да дешифрира бележката на Писети-Мориарти.

Умствената деградация на Холмс ставаше все по-застрашителна. Трябваше вече изцяло да се грижа за него. Доведох го в този тих селски кът, където живя в състояние, близко до тиха лудост, докато издъхна.

Погребах го в това уединено място, а на надгробната му плоча издълбах цифрите от диофантовия кинжал. Така завеща самият Холмс в минута на предсмъртно просветление.

Докторът замълча известно време, после каза:

— Не мега да забравя един от последните ни разговори, по-скоро един монолог на Холмс: „Целия си живот, Уотсън, съм играл из стражари и апаши и винаги съм бил стражар. Аз гонех, а от мене бягаха. Но колкото повече мисля за тази история с Писети-Мориарти, толкова повече и по-силно усещам, че не аз, а Мориарти е бил стражарят. Струва ми се, че този човек с желязна математическа логика е изчислил всичко. А аз съм си въобразявал, че разкривам и откривам, докато всъщност съм вървял по предварително начертан път. Почти съм убеден, че дори схватката край Райхенбахския водопад, с която толкова се гордеех, е била също програмирана в сценария.

Вие сте лекар, Уотсън и трябва да знаете, че в човешката природа се таи не само жаждата за живот, но жаждата за смърт. Обикновено жаждата за живот е по-силна. Но понякога има обстоятелства, когато жаждата за смърт надделява. Човек жадува смъртта си, но се страхува от обществото и религиозното порицание. И затова избира околни пътища. Жадуващият смъртта сам си избира палача и го заставя по един или друг начин да извърши убийството. В близкото минало най-лесният път е бил дуелът.

Впрочем, Уотсън, аз се отвлякох. Но аз също чувствувам, че съм бил избран за палач. У Писети — Мориарти е надделяла жаждата за смърт. Да направиш най-великото откритие и да не можеш да го покажеш пред хората! Гневен и объркан, той е тръгнал по своя трагичен път. Вече е нямало за какво да живее и той е измислил своя план — вие го знаете. Имал е нужда от един изключителен човек, за да го изпълни. И изборът му е паднал върху мене. Знаел е, че шифърът ще попадне именно при мен. И понеже ме бе свързал вече със себе си край водопада, Писети специално ми даде всички ключове за решаване на загадката. Той не използува възможността да направи шифъра си абсолютен, като приложи кода на Бодо. Ами самият шифър? Предлога, който може да се отгатне и без да се познава системата на шифриране, той зашифрира с уравненията на Питагор, Ферма и Ойлер. И шифрова със своето уравнение от детинство края на съобщението, което също е лесно за откриване. Но нито една ключова дума Писети не шифрова тривиално. Направил е така, че окончателното решение да принадлежи само на математик-професионалист, способен да се справи с нулево-параметричните диофантови уравнения в същия обем, както Писети-Мориарти. На първия етап му е бил нужен детектив. Сега, когато системата е разгадана, вече е необходим професионален математик. Той всичко е изчислил, целия мой път, първоначално палач, а после и детектив. Поставил ми бе указателни знаци и дори малки ободряващи сполуки, за да вървя ентусиазиран по този път. И аз стигнах до желязната математическа решетка, която, той е знаел, че не мога да преодолея.

Този истински сатана, италиански дявол! Как успя да ме измами!“

Минаха много години. Скоро ще навърша 70. Завърших университета. Станах математик-професионалист, дори професор в един от най-почетните университети. Целият ми живот протече под влиянието на тайната страст, бих казал порок, който ме разяжда: да се опитвам да реша проблема на Писети-Мориарти, тайната на шифъра. Но всичко бе напразно. Почти всичко. Защото с помощта на мощна ЕИМ успях да дешифрирам втория импулс от третата двуколонна буква и реших алтернативата на Холмс. Наистина това е най-дългата колонка. След като работи 10 часа, машината отпечата:

Следователно по системата за кодиране това е точка, а третата буква е „и“. Това е и моят принос в решаването на задачата. Повече от скромен в сравнение с онова, което стори детективът Шерлок Холмс. Затова реших да публикувам тези записки, нека всеки може при случай да опита собствените си възможности и сили. Може би ще се намери някой след Ферма и Писети, който да реши съдбовната задача, да изтегли кинжала от гърдите на Холмс и да върне на света мона Лутия.

Бележки

[1] Логиката е изградена върху оригинала, който е на руски език. ↑