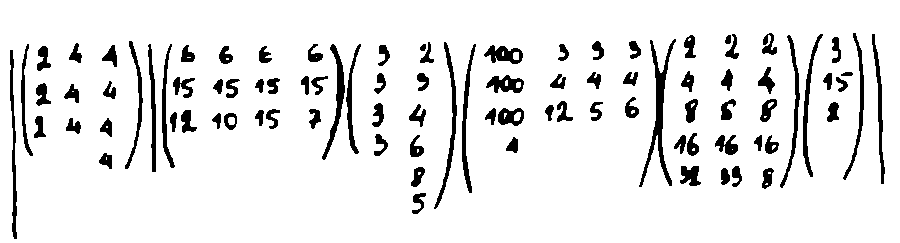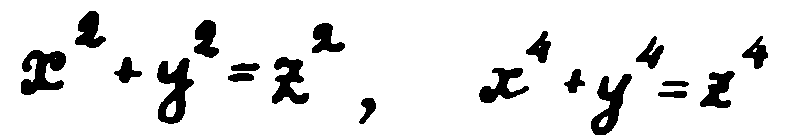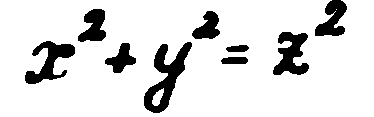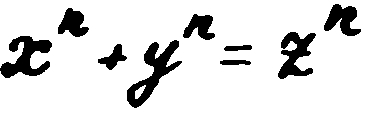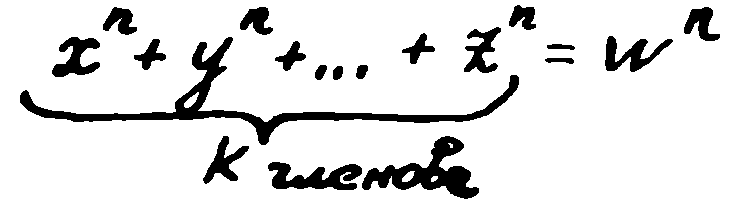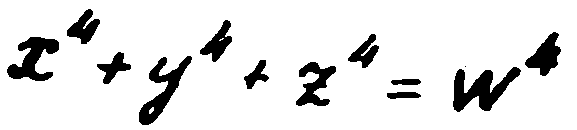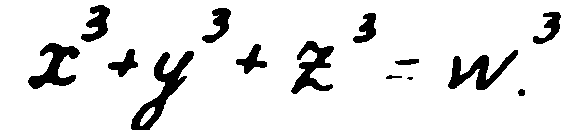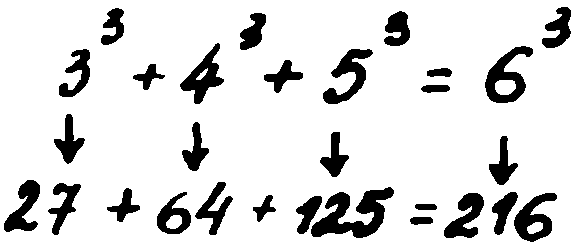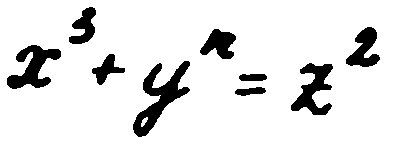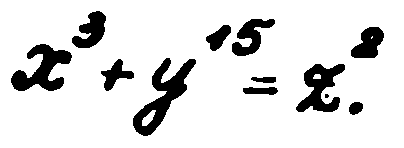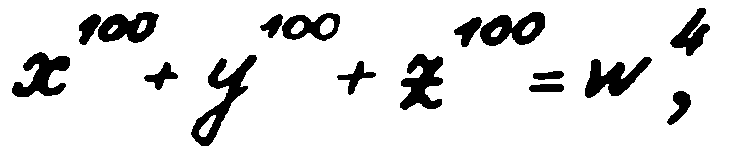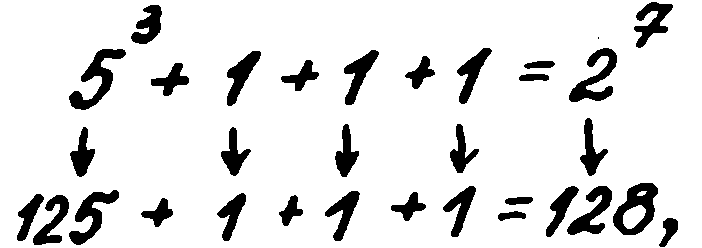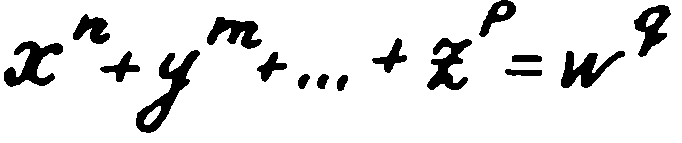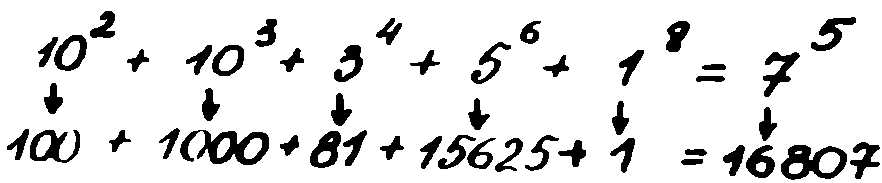Владимир Юровицки
Диофантовият кинжал

Когато се запознах с д-р Уотсън, той вече беше почти грохнал старик, самотен, сантиментален и общителен. Като много хора на неговата възраст той обичаше да си спомня за далечното минало, а аз с интерес слушах бавните разкази на доктора, посветени предимно на знаменития Шерлок Холмс.

Много неща от това, което чувах, ми бяха известни от публикациите на някой си м-р Конан Дойл, когото старецът явно не обичаше, въпреки че му признаваше известна живост на перото.

По него време Уотсън живееше в графството Чериуешир. Неговата скромна къща беше обкръжена от върбови гъсталаци, които бяха любимото място за нашите разходки. Бастунът на доктора разрошваше храсталаците, а самият той размотаваше дългата нишка на спомените. Може би след време ще доведа до сведенията на читателската публика някои нови истории за великия детектив, но сега ми се иска да ви разкажа само за една, която оказа съществено влияние върху моята съдба.

— Кажете ми, сър — казах веднъж аз, — как всъщност завърши дните си Шерлок Холмс? Нима просто се е състарил и починал като обикновен смъртен?

Уотсън потъна в дълбоко мълчание, което не се осмелявах да прекъсна. Накрая, сякаш отърсил се от нещо, докторът се изправи и без да каже дума, тръгна право към полето. Последвах го мълчаливо. Когато той спря, видях малка могилка от пръст, върху която беше поставена плоча. Върху плочата беше издялан надпис: ШЕРЛОК ДАЙРЕЙТИ ХОЛМС. Под нея следваха редица цифри. Те изиграха такава роля в цялата тази история и в моя живот, че ги запомних завинаги.

Уотсън стоя дълго с обронена глава, а след това показа плочата и тихо каза:

— Тук почива моят приятел, а тези цифри са автографът на неговия убиец.

— Как? — възкликнах аз. — Нима Шерлок Холмс е бил убит? Но кой тогава е този убиец? Ръката на правосъдието успяла ли е да го настигне?

— Той бе настигнат от наказваща десница и това беше ръката на самия Холмс.

— Извинете, сър, но как е възможно това? Въобще може ли убиецът да бъде убит от собствената си жертва?

— И въпреки всичко това е така. М-р Холмс бе погубен от злодей, когото сам унищожи цели десет години преди собствената си смърт.

— Но кой е тогава този убиец?

— Проф. Мариарти.

— Проф. Мариарти, който загина в схватката край Райхенбахския водопад? Невероятно!… А какво означават тези цифри върху камъка?

— Това е кинжалът, диофантов кинжал, който злодеят заби в гърдите на моя приятел. Нима би могъл някой да измисли толкова жестоко мъчение, ако не е бил изключителен злодей?

— Но защо тези цифри, този диофантов кинжал, както вие си позволихте да се изразите…

— Това е израз на самия Холмс.

— А защо те са издялани на гроба му?

— Хайде, младежо, да се върнем в къщи. Там ще ви разкажа цялата история във всички подробности.

И без да се обръща, Уотсън тръгна обратно. Бастунът му отново затрака глухо по сухата земя.

Седяхме пред камината. Разказът на стареца се разнасяше в полумрака и звуците сякаш се загубваха и стопяваха в тъмните ъгли. Тази обстановка и посещението на гроба на Холмс придаваха на чутото материална значимост и достоверност. Поради това и днес аз чувам всяка дума с всички интонации на старческия глас.

— В края на 19… г. бях принуден да напусна Лондон за няколко месеца във връзка с едно наследствено дело. Шерлок Холмс се намираше по това време в зенита на славата си. След ликвидирането на бандата на Мариарти той разкри още редица престъпления, след това откри няколко тежки съдебни грешки, което винаги му доставяше особено задоволство. Той не се гордееше с нищо повече, отколкото от спасяването на някой невинен от незаслужени страдания. Преди моето заминаване обаче Холмс нямаше никакви сериозни дела. Във времето му имаше „прозорец“ и той беше решил да го посвети на теоретична криминалистика. Тогава в Лондон широко беше разпространена модата да се пушат руски папироси с дълги мундщуци. Както е известно, този мундщук се прегъва. Холмс си беше поставил за цел да изследва връзката между характера на прегъването и облика на пушача. Размерът на сгъвката, казваше Холмс, е свързан с големината на пръстите, а последните добре корелират с ръста и телосложението на човека. Сдъвканият мундщук говори красноречиво за психическото състояние на пушилия и т.н.

Признавам си, че се отнасях скептично към новото увлечение на стария си приятел, но като си припомнях колко често моят скептицизъм биваше безпощадно посрамван, се стараех да не показвам това. Холмс по цели дни или скиташе по Лондон, събирайки по улиците угарки, или стоеше на Бейкър стрийт, изследвайки ги с микроскоп. Цялото жилище беше буквално затрупано от угарки, които разпространяваха чудовищно зловоние и предизвикваха мълчаливото негодувание на нашата мила хазяйка. Но Холмс беше толкова увлечен в своите занимания, в резултат на които трябваше да се появи солидна монография за угарките, че не забелязваше нищо, така както един лекар, открил ново лечебно средство срещу проказа, едва ли забелязва зловонията и ужасяващия изглед на своите пациенти. Така че заминавайки, бях напълно сигурен, че заниманията на Холмс с угарките ще заемат няколко години — той всичко правеше солидно и подробно. Когато се върнах на Бейкър стрийт обаче, открих пълна промяна на декорацията.

Угарките и микроскопите бяха изчезнали, а цялата стая на Холмс беше отрупана с… цифри. Върху масата, на дивана и креслата, на прозореца и бюфетите — навсякъде бяха разхвърляни листове хартия с цифри, цифри… Любопитството ми беше раздразнено, но не показвах това, знаейки от опит, че Холмс сам ще ми разкаже всичко, когато вече няма да бъде в състояние да пази тайна. На него му беше необходим събеседник, както на един философ — опонент. Така и стана.

След няколко дни при моето поредно посещение той се откъсна от своите изчисления, затвори прозореца, дръпна завесите и като седна в креслото, започна:

— Драги Уотсън, чувствувам, че вие изгаряте от любопитство. Сега ще ви разкажа някои неща, но предупреждавам, че това дело е изключително секретно. Спомняте ли си още за проф. Мариарти?

— Боже мой, че как мога да не си спомням. Споменът за двете ужасни години, които прекарах в оплакване на вашата гибел, и досега предизвиква потръпване в душата ми. Но какво би могло да се случи с него? Нима и той е възкръснал от мъртвите, както и вие на времето?

— Не, не, успокойте се. Той не е възкръснал или поне не е възкръснал физически. Независимо от това обаче неговото дело съвсем не е завършено. Проф. Мариарти беше шеф на цял престъпен синдикат. Действителността обаче многократно надмина нашите представи. Не без известна помощ от страна на вашия покорен слуга стана възможно да се разкрият истинските мащаби на тази престъпна организация. От полициите на много страни бяха арестувани участниците в тази най-голяма в цялата история на цивилизования свят банда.

Но сега не това ни интересува. Скотланд ярд успя да открие тайната щабквартира на организацията, създадена от проф. Мариарти в едно от незабележимите имения извън Лондон. При обиска бил намерен таен сейф, зазидан в стената.

В него сред различните уличаващи материали, благодарение на които се удаде да бъдат установени истинските размери на тайната организация и да се нанесе по нея съкрушителен удар, беше намерена една зелена папчица. Когато я отворили, агентите на Скотланд ярд едва не припаднали. Там се намирал опис на съкровищата, които тази организация награбила и струпала за десетилетията на своето съществуване. Тези съкровища са наистина неизчислими. Тук е и знаменитият рубин Такхо с тегло 1213 карата, принадлежащ на Тайската династия и изчезнал след превземането на Кохинхина от французите, брилянтът Шахур от съкровищницата на Тамерланд, многобройни по-малко прочути, но също изключително скъпи камъни: изумруди, сапфири, гигантски аметисти, в папката имало и пълен опис на гробницата на Туатесахон IX, която била открита само преди няколко години в Миса от знаменития археолог сър Кимридж, но оказала се малко преди това напълно разграбена. В описа са отбелязани златната маска на фараона, украшения от скъпоценни камъни, но най-ценното е над сто неизвестни на науката папируса. Трудно е да си представим каква стойност би имало за историците тяхното прочитане.

В съкровищницата на Мариарти се намират и уникални предмети от инкската и ацтекската цивилизация, безценни творби от майстори на Италианското възраждане, като например смятаната досега за безвъзвратно загубена прочута картина на да Винчи „Портрет на Мона Луция във виолетово“. Ще спомена още и картини, излезли под четката на Рафаел, Джорджоне, Джото, Ван Дайк, някои от които откраднати от Лувъра, Прадо, Ватикана и Дрезден, а други смятани за загинали.

Естествено, на езика ви се върти въпросът, дали тези съкровища са открити? Тъкмо тук започва ново действие на драмата. Беше установено, че местонахождението на съкровището е знаел само професорът и трима от неговите най-близки съратници. Случайно или поради нечий умисъл, днес всичките трима помощници на професора са убити, а и самият той загина в известната ви схватка. По този начин в момента нито една жива душа не знае къде се намира съкровището.

Независимо от всичко по принцип това не е особено обезкуражаващо. Работата е там, че в края на описа с ръката на самия професор било написано: „Мястото, в което се намира съкровището…“

И Холмс ми подаде една картичка, на която беше написано следното:

— Това е шифър — казах аз.

— Отгатнахте, Уотсън, това наистина е шифър. Но в края на краищата няма шифър, който да не може да бъде разчетен.

Срочно били мобилизирани най-добрите сили на Скотланд ярд и на други организации за разчитането на надписа. По-късно към тази работа внимателно били привлечени специалисти от САЩ, Франция и дори от генералния щаб на Руската империя, но уви, всичко било напразно. Специалистите в един глас заявили, че в случая е използувана абсолютно неизвестна система и техните методи са безсилни.

Тогава привлекли такива бележити математици като Хамилтън, Пуанкаре, Чатандрагар, но и те с нищо не могли да помогнат. Шифърът не се поддавал. И едва след това лично м-р-председателят се обърна към мене с молба да взема участие в това дело.

— И вие се съгласихте?

— Не без известни резерви. Казано честно, бях малко засегнат, че Скотланд ярд се мъчеше да ме отстрани от разследването, макар на вас вероятно да ви е чудесно известно каква беше моята роля в разгромяването на организацията, създадена от Мариарти. На м-р-председателя обаче не можех да откажа. А и честно казано, това не ми се и искаше. Преди всичко аз обичам костеливите орехи, а очевидно това е един от най-трудните. На второ място лично аз в схватката край водопада унищожих главния свидетел и смятам за мой морален дълг да направя всичко, за да върна на човечеството тези съкровища и най-вече на света усмивката на Мона Луция във виолетово.

— Разчитате ли, че това ще ви се удаде. Холмс?

— Имам такава надежда. Занимавал съм се малко с проблема на шифрите, спомнете си дори макар за танцуващите човечета.

— Добре, но сега? Намери ли се ключ към този шифър?

— Уви, скъпи ми Уотсън, от това очевидно още сме далеч. Но все пак съществуват и някои проблясъци.

С това нашият първи разговор приключи.

Върнахме се върху тайната на шифъра след две седмици, през които Холмс не напусна Бейкър стрийт и прекара времето, погълнат от изчисления.

— И така, Уотсън, нека разгледаме внимателно шифъра. Виждаме, че той се състои от цифри, които са обединени в шест блока или матрици, разделени с кръгли скобки. Блоковете имат различен брой редове и стълбчета, разположени линейно и разделени на два суперблока, заградени с вертикални черти.

Нека подходим към всичко това като към някакъв вид писменост. В теорията на писмеността се разглеждат обикновено следните видове:

1. Идиоматична писменост

2. Йероглифна писменост

3. Слогова писменост

4. Буквена писменост

При идиоматичната писменост всяка отделна единица изразява отделни фрази, които често са напълно завършени по съдържание. Пример за идиоматична писменост е кодът на радиолюбителите. Например в него ЩСА означава: „Аз ви чува така и така…“ К — край на предаването. Друг вид широко използувана идиоматична писменост са математическите символи. Точката означава, че две числа трябва да се умножат едно на друго, т.е. един цял завършен израз. При знак плюс стоящите редом числа се събират и т.н. Дори в нашата обикновена писменост, която се смята за буквена, присъствуват елементи на идиоматичната система. Това са препинателните знаци, които изразяват напълно завършени предписания за четящите.

При йероглифната писменост всеки знак означава дума. Това е най-древният вид писменост. Въпреки това и до ден-днешен тя се използува едва ли не от една трета от земните жители.

При слоговата писменост всеки знак означава отделен израз или определен устойчив звуков комплект. Слоговите системи в чистия си вид отдавна са отмрели, обаче останки от този вид писменост все още се съхраняват в някои езици. Не трябва да се отива далеч за пример. Буквата „а“ в едно изречение от нашия език означава дифтонга „ей“, т.е. дори цяла дума, а не само звук. Независимо от това едва ли Мариарти е използувал слоговата система. Тя е толкова архаична, че само специалист по археолингвистика би могъл да стигне до такова нещо. Поради това ние ще изключим слоговата писменост при по-нататъшните си анализи.

И накрая, връх в творческия гений на човека е буквената писменост, която преобразува оптимално звуковата информация в зрителна.

И така, първият въпрос е към какъв вид писменост се отнася нашето шифровано послание? Очевидно, че единица на тази писменост, неин знак е цифровият блок. Ако писмеността е идиоматична, то всеки блок е някакъв израз, цяла фраза. Така ние ще имаме шест фрази. Предполагам, Уотсън, че това е множко, за да се шифрова местонахождението на съкровището. По-нататък всички фрази са разделени от вертикални черти на две групи, като в едната се съдържа една фраза, а в другата — пет. Фактически се получават сякаш два абзаца или дори ако искате, два куплета. Но нали това не е стихотворение, нито разказ, даже не е и виц, за да се разбива на толкова едри семантични единици. По този начин ние можем напълно обосновано да заключим, че това не е идиоматична писменост.

Да предположим, че това е йероглифна писменост, т.е. всеки блок е символ, знак, йероглиф на няколко думи. Тогава разделянето с помощта на вертикални черти ни кара да предположим, че имаме работа с текст, състоящ се от две фрази, като първата фраза съдържа една дума, а втората — пет. Разбира се, съществуват и фрази от една дума. Като правило те са присъщи на устната реч и по-скоро повишават нейната изразителност, отколкото информативността й. Това са междуметия от вида „да“, „не“, и т.н. Ето защо имаме достатъчно сериозни основания, за да отхвърлим и тази хипотеза.

Така стигаме до последния вариант. Според него дадената писменост е буквена, а отделният цифров блок е буквен знак. Тогава съобщението се състои от две думи, едната от които може да бъде само предлог, тъй като се състои от една буква и се намира на първо място. Има само два еднобуквени предлога за място и посока — предлогът „с“ и предлогът „в“. По този начин ние вече научихме една от буквите с алтернативна точност. А втората дума съдържа пет букви.

— Наистина, Холмс, всичко това изглежда изключително убедително. Стига така да е мислел и Мариарти, това би било чудесно.

— Предполагам, че Мариарти въобще не се е замислял над този въпрос. Той е извършил шифроването като обикновен нормален човек, превеждайки чисто автоматично усвоената от него още през детството му писменост в друга писмена система. Но едва сега ние имаме основание за такъв извод.

— Добре, Холмс, но вероятно сега нещата ще тръгнат значително по-бързо. Спомням си, че при случая с танцуващите човечета вие приложихте честотния анализ и по този начин успяхте да разкриете шифъра. Смятам, че този метод може да се приложи и тук.

— Вие сте запомнили отлично тази трагична история. Наистина, че честотният анализ е най-мощното оръдие в ръцете на дешифратора. Изчислявате колко пъти в бележката се среща всеки знак, разделяте това число на общия брой на знаците в нея и получавате честотността на всеки знак. Честотният спектър на всички основни езици е добре проучен и са издадени специални таблици. Нещо повече, има таблици, които показват с каква честота се срещат не само отделните знаци, но дори и два знака заедно. Точно така се осъществява разшифроването на буквените шифри. Но спомнете си, Уотсън, с колко знака разполагах аз тогава?

— Ами не повече от стотина.

— Ето в това е и цялата работа. А сега аз имам само шест знака. А освен това нито един от тях не се среща два пъти и всички цифрови блокове са различни. Поради това в случая честотният анализ е безсилен.

— Тогава какво би трябвало да се направи, Холмс?

— Точно този въпрос и аз сам непрекъснато си задавам. И засега не намирам никакъв отговор. Някои неща ние вече знаем. Но те са твърде малко. Засега на нас не ни е известна шифровата система. И не знаем на какъв принцип една или друга буква е кодирана в цифровия блок. Необходимо е още да се поработи.

Нашият втори разговор завърши с това.

Третият ни разговор се състоя само след няколко дни. Холмс започна без заобикалки.

— Кажете ми, Уотсън, дали бихте могли да запомните над тридесет таблички от този род? — И той написа:

— Струва ми се, че не.

— Така си и мислех. Впрочем нещата не се състоят в обема на паметта на Мариарти.

Нека си припомним. Мариарти е бил учен. Той твърдеше, че е завършил някъде си университет, и от личните си контакти с него смятам това за напълно допустимо. Би ли могъл да бъде той толкова неразумен и алогичен, че чисто и просто да измисли за своята писменост таблички-азбука и самият той по най-тъп начин с тяхна помощ да шифрова текстове? Не. Отговорът ми е не! Логиката на учения не би допуснала това. Та самият стил на европейската наука изисква да се получават от минимум предпоставки максимум информация. Освен това би било необходимо някъде да се съхранява ключът за този шифър, т.е. на тази азбука, защото фактически е невъзможно тя да бъде запомнена наизуст. Следователно би се появила доста голяма вероятност или този шифър да бъде разкрит, или просто да се загуби ключът за него. Мариарти беше твърде умен, за да не разбира това. Какво следва от всичко дотук, Уотсън?

— Според мен, абсолютно нищо повече от това, което вие вече казахте, Холмс.

— Много неща, твърде много неща, мили мой докторе. Това означава, че всяка структурна единица, всеки цифров блок трябва да притежава собствена подструктура. Че блокът не е просто безсмислен комплект от цифри, а комплект с определен порядък и закономерност. Нима това не е откритие?

— Извинете ме, Холмс, но засега аз не виждам тук никакво откритие.

— Ех, Уотсън, Уотсън, за вас, медиците, логиката на цифрите е недостъпна. Но нима не е ясно, че е безсмислено да се опитваш да разшифроваш текст, ако всеки елемент е случаен, ключът е загубен и освен това няма никаква статистика. Но ако елементите на шифъра имат вътрешни закони, то задачата вече, изглежда, не е чак толкова безнадеждна.

— Нека разгледаме още веднъж цифровите блокове. Да се спрем на редовете. При отделни блокове те са абсолютно идентични, а при други блокове редовете прекъсват още на първия елемент. Да разгледаме и стълбчетата. Всички те тръгват от едно и също ниво и нямат никакви вътрешни прекъсвания. Няма нито едно абсолютно еднакво стълбче. Това вече е система. Докато при редовете съществува пълен хаос. Сега ясно ли ви е?

— Уви, не.

— Ама как може да не разбирате? Та това означава, че именно стълбчетата образуват информационната подструктура на блока, а не редовете. Че смисъл имат само стълбчетата и тяхната последователност, а не редовете. Че именно стълбчето съхранява известен квант информация, а съвкупността на тези кванти дава информация за буквата. Сега ясно ли вие, Уотсън? Всеки блок трябва да се чете по стълбчета, а не по редове.

— Сега е ясно. Но какво по-нататък?

— Нямам никаква представа. Но ще мислим. Този път ще мислим вече за стълбчетата. Защо те са с различна дължина и защо са с различно количество? Върху това вече може да се помисли, Уотсън.

През следващите няколко месеца срещах Холмс само от време на време. Той винаги бързаше за някъде. В къщи почти не се задържаше. Просто нямах представа каква работа го кара да се носи из околностите на Лондон и дори до доста отдалечени градчета. Бях сигурен, обаче, че това е свързано с тайната на Мариарти.

Най-сетне се състоя нашият четвърти разговор. Веднъж надзърнах на Бейкър стрийт и заварих Холмс изключително оживен.

— Уотсън, можете да смятате, че Мона Луция във виолетово вече виси ето на тази стена.

— Нима, Холмс, сте успели да разчетете шифъра на Мариарти? Поздравявам ви…

— Почакайте Уотсън, до това още не сме стигнали, но ключовете за шифъра са в ръцете ми.

— Ето вижте. — Той отново извади картончето с шифрованото послание.

— Какво бяхме успели да установим миналия път? Че всеки цифров блок трябва да се чете най-напред по стълбчета. Ние виждаме, че тук съществуват букви, съдържащи едно, две, три и четири стълбчета, т.е. от един до четири някакви си елемента. Така що за код е този, в който всяка буква може да бъде зашифрована чрез последователност от един до четири елемента?

— Честно казано, Холмс, не зная.

— Морзовият код. Та това е азбуката на Морз! Разбирате ли? Обикновената морзова азбука, при която всяко стълбче шифрова или точка, или тире, а последователността от тези точки и тирета дава кодът на буквата. Всичко е страшно просто, Уотсън. Тези няколко месеца аз посветих на изясняването на някои обстоятелства от живота на Мариарти в Лондон. Успях да открия една изключително важна подробност. В живота на професора е имало период, в който му се е наложило да се крие от своите собствени съучастници, тъй като в организацията му се била разгоряла борба за власт. В края на краищата Мариарти победил. Но в продължение на няколко месеца му се наложило да се крие. И както сега е вече установено, през това време той е служил в станцията на Бирмингамската железопътна линия като прост телеграфист. По тази линия и досега се използуват телеграфни апарати с морзовата система. Това е твърде важно за нас, тъй като в момента морзовият код в телеграфните съобщения навсякъде се измества от кода Бодо. И ако Мариарти би използувал за шифроване кода на Бодо, то нашите успехи биха били много по-проблематични. За щастие обаче той е знаел именно кода на Морз.

Вие често сте чували за кода на Морз, за морзовата азбука. В радиотелеграфията и най-вече в радиолюбителството тя и досега е основна. Морзовата азбука се състои от последователност от знаци, всеки от които може да бъде или точка, или тире. Количеството на знаците в различните букви е различно — от един до пет. Морзовият код се различава именно от това от кода на Бодо, че при последния всички букви имат точно пет знака.

Ето аз ще запиша морзовия код, за да може да следите по-лесно какво следва по-нататък.

Един знак има две букви, два знака — четири, три знака — осем букви, четири знака — 16 букви. Има една буква с пет знака, но това е рядката буква „з“, а такъв знак в това шифровано послание няма.

Един от знаците представлява стълбче в блока. Ние разполагаме с един блок от едно стълбче, един блок с две стълбчета, два — с три стълбчета, и два — с четири стълбчета. А сега нека да разгледаме шифрованото съобщение по-подробно. Вече допуснахме с добра степен на сигурност, че първата буква е „с“ или „в“. По всяка вероятност последният блок представлява окончания. Той е от едно стълбче. При един знак това може да бъде или буквата „е“, или „т“. Ако това е окончание, то по-вероятно е това да е „е“, отколкото „т“. Но с окончанието „е“ се свързва предлогът „в“.

От друга страна, буквата „в“ в морзовата азбука, както се вижда от таблицата, се състои от три знака. И в шифрованото съобщение първата буква се състои от три стълбчета, или с други думи, имаме пълно съвпадение. По такъв начин, изхождайки от морзовата азбука, получаваме, че първата буква е „в“, а последната „е“.

И така, както виждате, ние се придвижихме твърде далеч. Вече знаем две букви от шифъра и нещо повече, установихме, че стълбчетата 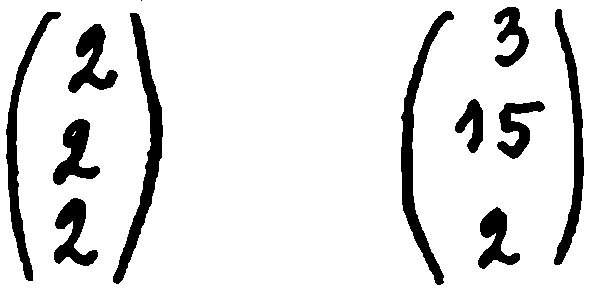означават точка, а стълбчетата 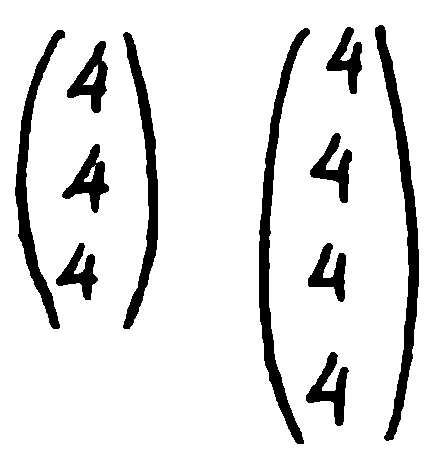означават тире.

— Да, Холмс, аз виждам, че вие действително не сте си загубили напразно времето и вече наистина сте близо до целта. Е, добре, а какво означават останалите тринадесет стълбчета, вече можете ли да ми кажете?

— Да, мога. Или точка, или тире. Засега обаче все още не мога да различавам точките от тиретата. Структурата на стълбчето ми е абсолютно неясна. На какъв принцип тройката от числа, 3, 15, 2 е отнесена към класата на точките, а тройката 4, 4, 4 към класата на тиретата, за мен е още загадка. Очевидно Мариарти е използувал някакво правило, с чиято помощ всяка последователност от цели числа може да се отнесе към един от тези класове. Говорейки на чист математически език, той е осъществил разлагане на някакво множество от цели числа на две непресичащи се подмножества и която и да е последователност от едно подмножество представлява знака точка, а от друго — тире. Но ние вече знаем четири образеца от това разбиване и аз кой знае защо съм сигурен, че разкриването на решаващото условие няма да представлява голяма трудност. Така че, Уотсън, подгответе стената за закачането върху нея на Мона Луция във виолетово.

Петият ни разговор се състоя след една или две седмици. Холмс беше изключително възбуден, което никак не съответствуваше на външността му на винаги сдържан джентълмен.

— Уотсън, струва ми се, че у мен се заражда една ужасна мисъл. А защо 2-2-2 да е „да“, а 4-4-4 да е „не“ („да“ да е точка, а „не“ да е тире)? Вчера като преглеждах сутрешния вестник на закуска — за какво се говореше в него, ще ви кажа после, — помислих си, а какво…, а какво би било, ако тези двойки или четворки се напишат по следния начин:

Вие, Уотсън, разбирате ли какво означават тези знаци?

— Разбира се. В колежа все пак съм държал изпит по математика и x, y и z са неизвестни числа. Те се степенуват на квадрат или на четвърта степен и се получава равенство.

— Точно така, Уотсън. Само че числата x, y и z трябва да бъдат цели, натурални — 1, 2, 5, 100 000, но не и 1,1 и не 0,95. И още едно малко „но“… Да не забравя. Чували ли сте нещо за Пиер Ферма?

— За съжаление, нищо.

— Тогава седнете и чуйте една от детективските истории в математиката. Във Франция през седемнадесети век живял юристът Пиер Ферма. Неговата истинска страст обаче била математиката и специално теорията на числата — разделът, който се занимавал със свойствата на натуралните числа.

На Пиер Ферма принадлежат множество първокласни резултати. Той например е доказал твърде важната Малка теорема на Ферма. По-голяма известност има обаче сред широката публика теоремата, която математиците, хора доста трезви, са нарекли тържествено и дори пищно Великата теорема на Ферма.

Известно е, че два квадрата могат да се съберат и да се получи квадратът на трето число. Това се е знаело още от древните египтяни. Така например числата 3, 4, 5 са се наричали именно египетски, тъй като

Казано с езика на математиката, равенството

може да се реши само с цели числа.

А ако сега вземем не втората степен на числата, а третата? Могат ли да се намерят две такива числа, които, като се повдигнат на трета степен и след това се съберат, да дадат число, представляващо на свой ред куб на някакво трето число? А ако такива числа за n=3 не съществуват, то при какви n съществуват такива числа? Така възникнал проблемът да се определи при какви n равенството

може да се реши с цели числа.

Пиер Ферма заявил, че не е възможно при никои други стойности на n освен 1 и 2 това равенство да се реши с цели числа. Нещо повече, той твърдял, че това съвсем не е предположение, а теорема, която е доказал с напълно математическа строгост.

Опитите на много математици да повторят доказателството или да намерят ново останали напразни. След смъртта на Ферма сред неговите документи намерили само бележка върху полето на една математическа книга, в която била приведена формулировката на теоремата за „нерешимостта“, а след това следвало: „Доказателството е твърде дълго, за да мога да го напиша тук.“ И повече нищо, нито ред повече на тази тема. Така и досега още не е известно дали Ферма наистина е доказал Великата теорема. Ще си позволя да споделя моето собствено мнение по този въпрос. Вие знаете, че аз макар и да не съм професионален математик, винаги съм бил любител на тази наука, тъй като моят дедуктивен метод изисква математически стил на мислене. И аз мисля, че Ферма е доказал теоремата. Работата е там, че тя е твърде необичайна за XVII век. По това време математиците са решавали задачи, а не са доказвали, че тяхното решение е невъзможно. Те са търсели корените на алгебричните уравнения на всяка степен, мъчели са се да разделят ъгъла на три части с пергел и линийка, да изчислят квадратурата на кръга и са се опитвали да докажат строго петия постулат на Евклид. Едва през деветнадесетия век било установено, че това са нерешими задачи. Но по това време подобен род мисли въобще не им е идвал на ум. Това е бил период на бурно развитие на математиката и задачите са се решавали една след друга. На фона на едни толкова забележителни успехи да предложиш хипотезата, че никой и никога няма да може да намери три такива числа, при които уравнението на Ферма да може да се реши при n, повече от две, е било психологически невъзможно. Подобна мисъл по това време би могъл да изкаже само онзи, който вече е имал за това твърдо доказателство. Следователно такова доказателство Ферма е имал. Аз съм сигурен в това.

Какво е то, доколко е сигурно и дали е достатъчно убедително от гледна точка на съвременната математическа придирчивост, не зная и не бих могъл да кажа. Това вече не е моя сфера. Най-поразяващото обаче е това, че и до този момент не е намерено не само доказателство за Великата теорема, но не е намерено дори и такова доказателство, което, макар и невярно, да би могло да бъде прието за истина от самия Ферма. Очевидно е, че това доказателство не е било чак толкова сложно, щом то не е намерило дори някакво отражение в неговата архива. Ако той би се занимавал с този проблем дълго време, то непременно в бележките му биха се запазили следи от тази работа. Очевидно Ферма е намерил решението така или иначе случайно, а ето вече цели триста години никой не може да го повтори. Истинско привидение в света на математиката.

Впрочем, Уотсън, аз сякаш се поувлякох. Но нека да продължим. Още от XVII век теоремата хвърля предизвикателство към математическия разум. Било проверено, че чак до n, по-малко от 2047, уравнението на Ферма наистина с цели числа е нерешимо. Но нали това не е отговор на поставената задача. А може би при n, равно на сто милиона, именно съществува решение.

Нов стимул за щурмуването на Великата теорема на Ферма се появи само преди няколко години, когато един германски индустриалец завеща един милион марки на онзи, който я докаже. За работа се захванали домакини и ученици, юристи (между другото самият Ферма също бил юрист) и шивачи, учители по математика и моряци от каботажния флот. Гьотингенският университет, на който според завещанието било възложено да се разпорежда с въпросната премия, бил буквално затрупан от „доказателства“. Уви, както и можело да се очаква, всички те се оказали погрешни.

Вестникът, за който обещах да ви разкажа, съобщава именно за това, че някакъв японски ученик бил доказал Великата теорема на Ферма, и математиците на Токийския университет не могли да намерят грешки в това доказателство. По всяка вероятност това е поредната фалшива вестникарска сензация.

Когато четях това съобщение обаче, бях пронизан от една мисъл. А дали Мариарти не е използувал Великата теорема на Ферма, за да шифрова съобщението? Та нали, ако последователността 2-2-2 се изпише като

то това означава, че даденото уравнение се решава с цели числа, т.е. принадлежи към класа на решимите уравнения на Ферма. Ние можем съответно да отнесем и самата последователност към специален клас. В същото време, ако вземем последователността 4-4-4 и я запишем като

то това уравнение не може да се реши в цели числа, което е доказано строго още от великия Ойлер. Поради това и самата последователност ние трябва да отнесем към друг клас. По такъв начин в дадения конкретен случай ние имаме последователности от различен клас. От друга страна, е известно, че първата последователност представлява знака точка, а втората — тире, ако първият блок наистина означава буквата „в“.

— Честно казано, Холмс, всичко това е ужасно интересно и смело. Но вие имате ли поне някаква сигурност, че всичко това е вярно?

— За съжаление, моята догадка е трудно да бъде потвърдена. Та нали само двете първи стълбчета подхождат за уравнение на Ферма. В останалите случаи или броят на членовете на уравненията са повече от три, или показателите на степените не са еднакви. И все пак, Уотсън, аз чувствувам интуитивно, че се намирам съвсем близо до ключа на шифъра. Нещо повече, преди до мен бяха достигнали слухове, че Мариарти е бил математик. Така че проблематиката във връзка с Великата теорема на Ферма сигурно му е била известна.

— Не бих могъл да добавя нищо, освен отново да повторя, че ужасно ми се иска да се окажете прав. Но нека, скъпи Холмс, все пак си позволя едно малко ехидство. Не ви ли се струва, че тук вие сменяте своя патентован дедуктивен метод на конкуриращия го индуктивен — от частното към общото?

— Ах, Уотсън, методът е важен, но резултатите са по-важни.

С това нашият пети разговор завърши.

Шестият ни разговор, както обикновено, започна с въпрос на Холмс.

— Известно ли ви е, Уотсън, кой е Диофант?

— Очевидно това е някакъв грък. Но в моето обкръжение ми се струва, че не е имало грък с такова име.

— Никак не се изненадвам. А причина за това е обстоятелството, че той е живял преди хиляда и петстотин години.

— Боже мой, Холмс, вашите търсения ви отвеждат в някакви бездни на историята. Преди беше в седемнадесети век, а сега чак в трети век. По този начин следващия път ще започнем от потопа и Ноевия ковчег.

— Уви, докторе, за да разгадаем тази тайна, на нас ни се налага наистина да се вглъбим в твърде далечни времена. И така този грък Диофант е бил много голям математик. Един от първите той е описал уравненията, наречени на негово име, и при които отговор могат да бъдат само натурални числа.

Ето ви едно най-просто Диофантово уравнение. Необходимо е да се разделят пет ябълки на трима души, но така, че на всекиго да се падне поне по една ябълка.

Алгебричното решение на това уравнение е просто: всеки получава своя справедлив дял — по една ябълка и две трети. Но в системата на Диофант този отговор не е верен, тъй като в нея ябълките не се делят. Значи ние можем да дадем на двамина по две ябълки, а на един — само една ябълка. Или пък на двамина — по една, а на третия — три. Така за разлика от обикновената алгебра, където решението е едно-единствено, в Диофантовата алгебра съществуват няколко решения. Но може да има и само едно решение например, ако пет ябълки трябва да се разделят на пет души, а може да няма и нито едно решение, ако пет ябълки трябва да се разделят на шест души.

И така уравнението на Ферма също представлява Диофантово уравнение, само че от по-висока степен. Но освен уравненията на Ферма с две събираеми в лявата си част, са били разглеждани и по-общи уравнения. Леонард Ойлер е изучавал например следните уравнения:

Той е смятал, че тези уравнения не могат да имат Диофантово решение при k<n, т.е., ако броят на събираемите в лявата част е по-малък от показателя на степента в уравнението.

Уви, и това твърдение не е нищо повече освен една хипотеза, но като се има предвид, че тя е била създадена от самия Ойлер — математик с поразителна интуиция, ние можем да се доверим напълно на думите му.

И така третият знак — тирето в предлога „в“, с който започва текстът, се изразява именно с четири четворки, т.е. представлява Диофантово уравнение —

Съгласно хипотезата на Ойлер то не може да има Диофантови целоцифрени решения, тъй като броят на събираемите в лявата му част е 3 — по-малко от степента на уравнението — 4. Според моето предположение за кодирането на съставките това е именно тире, както ние определихме по-рано. Това е още едно потвърждение на хипотезата за използуваното от Мариарти правило за решаване: ако имаме решение с цели числа, то това означава отговора „да“, т.е. стълбчето означава точка, а ако няма такова, то и отговорът е „не“, т.е. стълбчето е тире.

Но ние можем да отидем и по-нататък. Да разгледаме сега третата буква на шифъра. Тя се състои от две стълбчета, т.е. има само две съставки. Ако разгледаме морзовата азбука, ще видим, че от шест гласни, две букви — една трета — имат именно две съставки. От друга страна, две съгласни от двадесет и шест също имат две съставки, но тук вероятността е равна на 1/13. Какво следва от това? С вероятност от 80 процента третата буква е гласна.

Такива гласни има две — „а“ и „и“. Едната има в морзовата азбука две точки, а другата — точка и тире. И двете имат в началото точка. Съгласните започват с тире. Първото стълбче на тази буква е 3-3-3-3, т.е. според нашата хипотеза, отговаря на Диофантово уравнение

Тук броят на събираемите в лявата част е равен на степента — събираемите са три и степента е три. Хипотезата на Ойлер не казва нищо за възможността подобни уравнения да се решават с цели числа. Но ние и сами можем да открием, че за това уравнение съществува Диофантово решение. И наистина:

По този начин според нашето правило това стълбче трябва да изразява точка, което ние всъщност установихме, като изходихме от съвсем други съображения. Това вече съвсем не може да е случайно. И така ние вече знаем с абсолютна точност две букви и трета буква с една алтернативна точност.

— Напредъкът е наистина добър. Но, Холмс, а ако внезапно се окаже, че вие въпреки всичко се намирате на погрешен път? Това би било такова разочарование, че дори се страхувам да мисля за това. Та нали ако се разгледат останалите стълбчета, при тях не се среща нито последователността на Ферма, нито последователността на Ойлер. В такъв случай какво би могло да означава стълбчето 2-3-4-6-8-5? Как да се приложи спрямо това стълбче вашата теория?

— Самият аз имам много съмнения. Необходимо е да се научи всичко за Мариарти. Убеден съм, че неговата биография ще ни даде последния ключ към тази загадка.

С тези думи завърши нашият шести разговор.

След този ни разговор Холмс изчезна за дълго от бреговете на мъгливия Албион. Получавах от него кратки писъмца от Италия, Франция и Германия. В тях той съобщаваше без подробности, че нещата се придвижват и се появяват нови интересни факти. Изминаха две години и можете да си представите моята радост, когато, разхождайки се по Бейкър стрийт, забелязах, че скъпият за мене прозорец свети.

Холмс беше загорял и стегнат. Въпреки неговия блестящ вид обаче аз почувствувах у него някакво напрежение и дори несигурност, която беше толкова неприсъща на моя приятел.

— Скъпи Холмс — започнах аз, — донесохте ли вече със себе си Мона Луция в оранжево? Какви успехи имате във вашите изследвания?

— Това беше едно много успешно пътуване, Уотсън. Убедих се напълно в правилността на моя метод за дешифриране. Но можах да науча и нещо, което за първи път ме накара да се замисля дали моята дейност е винаги за благото на хората. Усъмних се в своята правота, Уотсън.

— Боже мой, Холмс, какво толкова трагично сте могли да научите в областта на някакви си диофантови уравнения? Нима и в математиката може да има трагедии?

— Вие смятате, че хармонията на числата и математическите абстракции са лишени от човешките страсти. Това е голямо заблуждение. Широката публика е убедена, че математиците са студени хора, които стоят неподвижно зад бюрата си и пресмятат безстрастно, извеждайки като автомати някакви неразбираеми формули. Колко далеч са от истината подобни представи.

Ето ви например историята на даровития младеж на име Джакомо Писети. Той се е родил в семейството на преподавател по математика в Сицилия. Още от детските си години Джакомо проявявал забележителни математически способности. Това станало ясно, когато петгодишният Джако, така го наричали в къщи, открил грешка в някакви изчисления на баща си, които той бил подготвил за поредната си лекция. От този момент главата на семейството започнал да прави всичко за развиването на тази способност у детето. Джако се интересувал специално от теорията на числата, впрочем това е обичайната сфера на интереси за всички вундеркинди в математиката. И, разбира се, той не можал да отмине незабелязано край Великата теорема на Ферма. На 15 години той доказал, че уравнението

е решимо в цели числа при всякакви n.

Ходът на разсъжденията му бил по принцип прост, но разкривал оригиналното мислене на младежа. Тъй като 2³+1ⁿ=3², то това може да се запише като

Но единицата при всякаква степен си е единица и той намерил израз на същото равенство под формата 2³+1=3² и така получил своята теорема

— Почакайте, Холмс. Аз неволно започнах да се замислям върху вашия шифър. Дори можах да забележа, че последното стълбче е 3-15-2 и фактически представлява уравнението на младия Джако.

Но ако то се решава с цели числа, когато x=2, y=1, а z=3, то това стълбче означава точка и това е стълбчето „да“.

— Уотсън, дори и не съм помислял, че сухата математика може да увлече дори и вас. Впрочем вие сте напълно прав. Нещо повече, тъй като последното стълбче означава още и буква, то тази точка означава буквата „е“, което ние определихме още по-рано от чисто граматични съображения. Както виждате, всичко съвпада по най-добър начин.

— Но какво отношение има младият Джако към нашия шифър?

— Почакайте малко, Уотсън, аз продължавам. И така, Джако завършва училище със златен медал. Предсказват му бляскаво бъдеще. Той постъпва в Палермския университет, но след една година учение професорът по математика заявява, че той не може да даде нищо повече на младежа и му препоръчва да се прехвърли в някой от най-известните университети. Отчитайки склонността на Писети към теорията на числата, той го насочва към Гьотингенския университет, където четял лекции великият Давид Хилберт и преподавал Ернст Кумер — създателят на теорията за алгебричните числа. Между другото той създал тези числа именно по време на неудачния си опит да докаже Великата теорема на Ферма.

Дори в Гьотинген, където е трудно да изненадаш някого с математическо дарование, Джакомо се отделял със своите способности. Неговата научна работа ръководел самият Кумер и интерес към нея проявявал дори великият Хилберт. Джакомо продължавал да работи върху Великата теорема на Ферма. Но като разбирал безнадеждността на фронталния щурм на тази твърдина, отчитайки опита на своя учител Кумер, той предприел широка обходна маневра. Писети започнал да разглежда много по-общи уравнения от Ферма и Ойлер, т.е. уравнения от типа

с всякакви цели степени n, m, p, q и с всякакви броеве на членовете. Той ги нарекъл нула-параметрични диофантови уравнения.

Лесно е да се види, че и уравнението на Ферма, и уравнението на Ойлер са само частни случаи на нула-параметричните диофантови уравнения.

Писети си поставил за цел да намери критерий за решаемостта на произволните нула-параметрични диофантови уравнения. И в този момент младият човек се върнал към своята детска работа. Та той още и по-рано бил забелязал, че решения от типа на онова, което намерил някога, дават критерий за решаемостта на цял клас нула-параметрични диофантови уравнения. От факта, че е вярно следващото

следва, че уравнението

е решимо в цели числа при всякакви n, m, p. Решенията на нула-параметричните уравнения, в които поне едно от неизвестните е равно на единица, по-късно дори получили името решения на Писети.

Продължавайки своите занимания, Джакомо открил, че между решимите диофантови уравнения и решенията на Писети има определена взаимовръзка. Той доказал или му се сторило, че е намерил доказателство, според което всяко решимо нула-параметрично диофантово уравнение може да се съпостави с някои от решенията на Писети.

А по-късно той успял да докаже, че уравненията на Ферма при n по-голямо от две не може да се постави в съответствие с нито едно от решенията на Писети. Това вече било победа. Нещо повече, това бил истински триумф. Великата теорема на Ферма паднала. Можете ли да си представите какво е изпитвал щастливият младеж, когато изведнъж разбрал, че е победил тази тристагодишна твърдина.

Доказателството било проверено най-прецизно от Кумер. След това то било представено на самия Хилберт. Той не успял да намери в него нито една пукнатинка и лично изпратил тази работа за публикуване в най-доброто математическо списание „Математически анали“.

Но когато статията вече била набрана, когато книжката на списанието вече можела да се появи на пазара всеки момент, оповестявайки на света за раждането на нов математически гений, най-близкият приятел на Писети, един почти невръстен математик от Русия, открил в доказателството грешка. Статията била срочно изискана обратно, наложило се списанието да се препечатва, а великият Хилберт бил извън себе си от възмущение, защото едва не станал за посмешище по вина на някакво си италианско момче… А можете да си представите какво преживял младият Джако Писети. Той бил разтърсен от най-дълбока душевна травма и се наложила неотложна психиатрична помощ. Той излязъл от болницата слаб, бледен и озлобен на целия свят. Повече за Джакомо Писети в математическите кръгове никога и никой не чул…

— Искате да кажете, Холмс, че в замяна се появил професор Мариарти?

— Да, Уотсън. Решенията на Писети и досега живеят с математиката. Но никой повече не е чул за самия Писети. Той умрял. И се родил великият злодей професор Мариарти.

— Но как той е могъл да стане това?

— Това е все още в много отношения загадъчна история. Не забравяйте, че Писети произхожда от Сицилия. Както успях да установя, неговият чичо е бил един от главатарите на тамошната мафия.

— Да, Холмс, прав сте, че това е една ужасна трагедия. Великата теорема на Ферма е осакатила живота на този талантлив млад човек и го е отвела в края на краищата в Райхенбахската клисура. Но всичко това хвърли ли някаква светлина върху шифъра?

— В определена степен, да. Та вие сам забелязахте, че в шифъра е използувано детското уравнение на Джакомо Писети. Не е възможно тук да съществува някаква случайност. Сега вече ни е известна най-точно системата на шифроването. Необходимо е да се вземе едно стълбче, например първото стълбче на четвъртата буква 100–100–100–4 и да се състави с него нула-параметричното диофантово уравнение

да се определи има ли това уравнение решение в цели числа и ако да, то тогава това означава точка, а ако не — тире. Като извършим тази операция с всички стълбчета на цифровия блок, ние ще получим кода на Морз — буквите. А като определим всички букви, ще научим къде се намира съкровището.

— И вие вече сте направили това?

— Уви, Уотсън, и в това се крие тайната. Всички математици, с които разговарях в Гьотинген, Сорбоната и Оксфорд, твърдят единодушно, че проблемът за решаемостта на онези диофантови уравнения, които им давах, изхождайки от шифъра, не са по силите на съвременната математика. На пръв поглед изглежда, че могат да се намерят решения на тези уравнения чрез просто надбавяне. Но в написаното по-горе уравнение дори и най-малкото число — 2¹⁰⁰ — има 30 (!!!) знака и никакво такова изчисляване не е възможно не само на ръка, но дори и с появилите се в последно време механични изчислители. Вече знаем всичко за шифъра и въпреки това сме безсилни.

— Но нали Мариарти… или може би по-точно Писети все пак е шифровал по някакъв начин. Той не може да не е знаел кои уравнения са решаеми и кои не.

— Уотсън, точно тук ние се приближаваме до най-загадъчната част в цялата история. От своите разговори с математиците си извадих заключението, че да се шифрова този текст е възможно само ако знаеш точно условията за решимостта на всички, подчертавам, всички нула-параметрични диофантови уравнения. Следователно като минимум трябват доказателствата на Великата теорема на Ферма.

— С други думи казано, ако съм ви разбрал правилно, Мариарти, по-точно, Писети-Мариарти е доказал Великата теорема на Ферма.

— Да, да, Уотсън. От този шифър това следва с абсолютна неизбежност. Той е доказал и Великата теорема на Ферма, и хипотезата на Ойлер, и дори нещо повече от това — условията за решимостта на всички нула-параметрични диофантови уравнения.

— Божичко… Но това означава… това означава, че Мариарти, или Писети, е наистина един от най-великите математици на всички времена… И в същото време е един изключително голям престъпник… Наистина тук има от какво да се побърка човек, Холмс. И все пак не е ли възможно във всичко това да има някаква грешка?

— Не може да има никаква грешка. Работата е там, че той е решил съвсем различна задача от тази, която са решавали всички. Можеш да спориш колкото ти се иска за доказването на Великата теорема — достоверно ли е то или не — от това нейната правота не зависи. Но ако вие сте извели условията за решаемостта на което и да е нула-параметрично Диофантово уравнение, то да се намери грешката е нещо тривиално. И освен това не забравяйте колко жестоко е платил на времето Писети за своята грешка. Просто е немислимо той да я направи втори път. Психологически е немислимо.

— Наистина, аз само мога да повторя, че тук има от какво да се побърка човек, Холмс.

— Да, представете си, аз всъщност напоследък си представям всичко това доста често. Поруган и осмян, Писети потъва в бездната на престъпния свят, за да отмъсти на хората за своя позор. Той измисля и осъществява най-дръзки престъпни акции. За миналия си свят той вече не съществува. Дори и не иска да го знае и да си спомня за него. Но младежките му мечти за Великата теорема го спохождат отново и отново. Той ги прогонва, но напразно. И ето че в някакъв момент на тази борба, отчаян от схватката между миналото и настоящето, той бива споходен от мигновено озарение. Пред него пламнала светлина — и той видял. Какво ли е изпитвал в този момент? Перото на Шекспир и на Достоевски вероятно би могло да опише това. Но аз съм само един детектив.

А след това, когато се успокоил, той разбрал, че никой няма да научи за неговото откритие. За него вече нямало път назад, в нашия свят, в това число и в света на науката. Той не можел да оповести своето доказателство, тъй като щял да разкрие себе си, тъй като под каквото и име да би го публикувал, Хилберт, Кумер и неговият руски приятел, постигнал по това време в родината си големи успехи и почести, във всички случаи щели да разберат, че зад това стои Писети. А може би му е била непоносима самата мисъл отново да подлага плодовете на душата си на съда на същия този Хилберт.

И тогава той решава да създаде собствена награда за онзи, който постигне същото като него, и в същото време да подсигури своя приоритет по най-необикновен начин. Това трябвало да бъде една феноменална награда. И той с още по-голямо усърдие започва да се занимава със своята организация, която граби, краде, прекупва безценни съкровища и попълва своето богатство, което ще се падне на онзи, който съумее да разшифрова неговите записки, т.е. да реши същата задача, вече решена от него.

А и тази схватка в Рейхенбахската клисура. Тя още е пред очите ми. Кого всъщност блъснах в пропастта — един велик злодей, или пък гениалния математик?

— Но, Холмс, нали вие не сте имали никаква възможност за избор. Или вие него, или той вас.

— А нима това не е възможност за избор? Както и да се оправдавам, но фактът си остава факт. Аз убих най-великия човек в историята на математиката.

— Но в същото време и най-великия злодей.

— Не, математик. Та Писети…

— Мариарти, Холмс.

— Нека бъде Писети-Мариарти… Впрочем какво исках да кажа? Да, Уотсън, аз чувствувам, че всичко, което научих, е извършило у мен някаква промяна. Аз чувствувам, че у мен детективът е умрял. Та нали, за да осъществяваш правосъдие, дори само за да способствуваш за неговото осъществяване, трябва да си абсолютно убеден, че твоите представи за доброто и злото и твоето понятие за справедливост не си противоречат и са еднозначни, че те не могат да станат на свой ред източник на зло. А днес вече не съм така сигурен в това, както преди.

— И какво се готвите да правите сега?

— Аз съм длъжен да направя всичко, за да върна на човечеството тези съкровища и същевременно поне отчасти да възстановя истината за Писети-Мариарти.

— Но нали вие не сте математик, Холмс. Ако професионалните математици са безсилни, то какво можете да направите вие?

— Правилно, Уотсън, аз не съм математик. Обаче Писети е намерил пътя. А да вървиш по него е хиляди пъти по-лесно, ако знаеш, че целта е постижима.

Но има и друг път за разкриването на шифъра. За да можеш да откриеш тирето, необходимо е да направиш същото, което е направил и Писети. Но да разшифроваш точката може, просто намирайки поне едно частно решение, съответствуващо на Диофантово уравнение. Това може да се постигне чрез тъпо прехвърляне на различни варианти. И ако се удаде по този път да откриеш поне няколко знака-точки, то имайки правилата на граматиката и морзовия код, можеш да получиш напълно обозрими варианти за прочитане на текста. Тук е необходим късмет, Уотсън.

Така и завърши нашият седми разговор.

След това имахме и други разговори, много разговори, но те вече не представляват интерес. Остава ми само да съобщя епилога. Шерлок Холмс изостави напълно криминалогичната дейност. Остана незавършена дори неговата монография за угарките. Той се занимаваше само с теорията на числата. В минути на отчаяние Холмс горчиво се оплакваше, че Писети-Мариарти е забил в него диофантов кинжал.

С тъга наблюдавах угасването на мощния някога интелект, изнуряван от безкрайни изчисления и непрекъснати математически сметки, обхванат от всепоглъщаща страст, от манията да дешифрира шифъра на Писети-Мариарти.

Постепенно признаците на умствената деградация на Холмс ставаха все по-застрашителни. Наложи ми се да поема всички грижи по него. Прехвърлих го в този селски кът, където той живя в състояние, близко до тиха лудост, до самата си смърт.

Погребах го в уединено място и върху надгробния му камък издялах рисунка на диофантовия кинжал. Това беше в съгласие със завещанието на Холмс, което той направи в мигове на предсмъртно просветление.

Като помълча малко, докторът добави:

— Не мога да не си припомня един от нашите последни разговори. Той беше по-скоро монолог на Холмс. „Целия си живот, Уотсън, аз пропилях в игра на «апаши и стражари» и винаги в нея бях стражарят. Преследвах и бягаха от мене. Но колкото повече мисля за тази история с Писети-Мариарти, все повече и повече усещам, че не аз съм бил стражарят, а Мариарти. У мен се утвърждава впечатлението, че този човек с желязна математическа логика е пресметнал всичко, а аз, мислейки, че разкривам и търся, всъщност съм вървял по предварително програмиран път. Почти съм убеден, че схватката при Рейхенбахския водопад, с която се гордеех толкова, също е била по програмиран сценарий.

Вие сте лекар, Уотсън, и не може да не знаете, че в човешката природа се таи не само жаждата за живот, но и жаждата за смърт. В повечето случаи жаждата за живот е по-силна. Обществото прави всичко възможно, за да подтисне сред своите членове инстинкта за смъртта. Всички религии също забраняват и рязко осъждат самоубийството. Но има натури и има обстоятелства, когато жаждата за смърт побеждава. Случва се, и то доста често, човек да жадува смъртта, но да се страхува от религиозното и общественото осъждане. И често да избира заобиколни пътища, за да задоволи своята жажда за смърт. Колко младежи, разочаровали се в любовта и готови без разсъждения да изпият чаша отрова, вместо това отиват на война, хвърлят се в огън и дим и извършват геройски постъпки именно защото животът не им е скъп повече.

Има обаче и още по-кошмарен вариант. Жадуващият смъртта си подбира и собствен палач и го заставя по един или друг начин да осъществи убийството. Най-простият път към това, особено в недалечното минало, беше дуелът. Застрашавайки го с пистолета си, замаскираният самоубиец заставя избрания от него палач да изпълни страшното дело.

Впрочем, Уотсън, аз сякаш се отвлякох. Но и аз се чувствувам като човек, който е бил избран за палач. След всичко случило се с Писети-Мариарти аз се съмнявам, че у него е останала някаква жажда за живот. Да направиш велико откритие и да нямаш възможност да се представиш с него пред хората! В гняв и смут той тръгнал по своя трагичен път. Но след това тези чувства у него изчезнали. Нямало вече за какво да живее и той замислил своя план, който вече знаете какъв е бил. На него му бил необходим не съвсем обикновен човек, който да поеме върху себе си изпълнението на замислените от него планове. Изборът му паднал на мене.

Той е знаел, че именно у мене ще попадне неговото шифровано съобщение, тъй като вече ме бил свързал със себе си още край Рейхенбахския водопад. Писети ми е дал нарочно ключовете за разгадаването. Поради това той не използувал възможността да направи своя шифър абсолютен, прилагайки кода на Бодо. А самият шифър! Той е предлог, който би могъл да се отгатне и без да знаеш системата му. Той е зашифровал уравненията на Питагор, Ферма и Ойлер. Зашифрова своите детски уравнения с окончание, което се разгадава също доста просто.

Но нито една ключова буква Писети не е зашифровал тривиално. Той е направил всичко, за да може окончателното решение да бъде намерено от математик-професионалист, който да се справи с проблема за нула-параметричните диофантови уравнения в същия обем, както това успял да направи Писети-Мариарти. През първия етап му е бил необходим детектив. А сега, когато системата на шифъра е разгадана, аз вече не съм му необходим, нужен му е математик-професионалист. Той е пресметнал всичко, целия мой път, първоначално на палач, а след това на детектив. Разположил е за мене стълбове и дори малки ободряващи знаци, за да мога да вървя по набелязания път с ентусиазъм. И аз достигнах… до една желязна математическа решетка, която, той е знаел със сигурност, че не е по силите ми. Той е истински сатана, истински дявол, как само можа да ме подмами!“

Минаха много години. Скоро ще навърша 70. Завърших университета. Станах математик-професионалист и дори професор в един от най-почтените червенотухлени университети. Но целият ми живот протече под давлението на тайна страст, дори бих казал порок, който ме изсушаваше и угнетяваше под гнета на опитите да реша проблемата Писети-Мариарти, да разкрия тайната на шифъра. Но всичко беше напразно. По-точно, почти всичко. Тъй като освен извършеното от великия детектив аз успях с помощта на мощна ЕИМ да дешифрирам втория знак на третата буква от две стълбчета, да реша алтернативата на Холмс. Наистина това е най-дългото стълбче: 2–3–4–6–8–5. След като работи десетина часа, компютърът най-сетне подаде:

Според системата за кодиране това следователно е точка, а самата трета буква излиза, че е „и“. Ето това е целият мой принос в тази задача. Вярно е, че той е твърде скромен за математик със световно име в сравнение с онова, което е направил детективът Шерлок Холмс. И поради това реших да публикувам тези бележки, за да може всеки да опита своите сили. Може би ще се намери още някой след Ферма и Писети, който да реши тази съдбоносна задача, и измъквайки кинжала от гърдите на Холмс, да върне на света Мона Луция в лилаво.^[1]

Бележки

[1] В крайна сметка през 1995 година Великата теорема на Ферма била обявена за окончателно доказана, като доказателството се разпростирало на повече от сто страници и ползвало неизмеримо по-сложен математически апарат от нужния за формулирането. — бел.ел.кор. ↑